题目内容
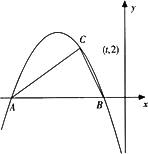
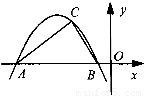
如图,已知二次函数y=x2-2x-1的图象的顶点为A.二次函数y=ax2+bx的图象与x轴交于原点O及另一点C,它的顶点B在函数y=x2-2x-1的图象的对称轴上.(1)求点A与点C的坐标;
(2)当四边形AOBC为菱形时,求函数y=ax2+bx的关系式.

【答案】分析:(1)配方可得顶点A的坐标,又可得所以点C和点O关于已知二次函数图象的对称轴l对称,可得C的坐标;
(2)由题意可得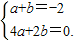 ,解之可得a、b的值,可得所求.
,解之可得a、b的值,可得所求.
解答:解:(1)配方可得y=x2-2x-1=(x-1)2-2,所以顶点A的坐标为(1,-2).…(2分)
因为二次函数y=ax2+bx的图象经过原点,且它的顶点在二次函数y=x2-2x-1图象的对称轴l上,
所以点C和点O关于直线l对称,所以点C的坐标为(2,0).…(6分)
(2)因为四边形AOBC是菱形,所以点B和点A关于直线OC对称,因此,点B的坐标为(1,2)…(9分)
因为二次函数y=ax2+bx的图象经过点B(1,2),C(2,0),
所以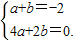 ,解得
,解得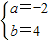 …(13分)
…(13分)
所以二次函数y=ax2+bx的关系式为y=-2x2+4x.(14分)
点评:本题考查二次函数的性质,涉及数形结合的思想,属基础题.
(2)由题意可得
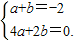 ,解之可得a、b的值,可得所求.
,解之可得a、b的值,可得所求.解答:解:(1)配方可得y=x2-2x-1=(x-1)2-2,所以顶点A的坐标为(1,-2).…(2分)
因为二次函数y=ax2+bx的图象经过原点,且它的顶点在二次函数y=x2-2x-1图象的对称轴l上,
所以点C和点O关于直线l对称,所以点C的坐标为(2,0).…(6分)
(2)因为四边形AOBC是菱形,所以点B和点A关于直线OC对称,因此,点B的坐标为(1,2)…(9分)
因为二次函数y=ax2+bx的图象经过点B(1,2),C(2,0),
所以
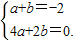 ,解得
,解得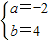 …(13分)
…(13分)所以二次函数y=ax2+bx的关系式为y=-2x2+4x.(14分)
点评:本题考查二次函数的性质,涉及数形结合的思想,属基础题.

练习册系列答案
相关题目
 如图,已知二次函数y=x2-2x-1的图象的顶点为A.二次函数y=ax2+bx的图象与x轴交于原点O及另一点C,它的顶点B在函数y=x2-2x-1的图象的对称轴上.
如图,已知二次函数y=x2-2x-1的图象的顶点为A.二次函数y=ax2+bx的图象与x轴交于原点O及另一点C,它的顶点B在函数y=x2-2x-1的图象的对称轴上.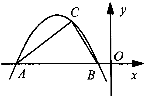 如图,已知二次函数y=ax2+bx+c(a,b,c为实数,a≠0)的图象过点C(t,2),且与x轴交于A,B两点,若AC⊥BC,则a的值为
如图,已知二次函数y=ax2+bx+c(a,b,c为实数,a≠0)的图象过点C(t,2),且与x轴交于A,B两点,若AC⊥BC,则a的值为