题目内容
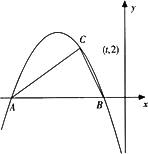
如图，已知二次函数y=ax2+bx+c（a，b，c为实数，a≠0）的图象过点C（t，2），且与x轴交于A，B两点，若AC⊥BC，则a的值为 ．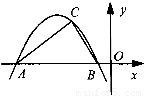
【答案】分析：设A（x1，0），B（x2，0），由题意可得t2+bt+c=2，由AC⊥BC，可得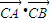
=（x1-t，-2）•（x2-t，-2）=0，代入根据方程的根与系数关系可求a
解答：解：设A（x1，0），B（x2，0）
∵二次函数y=ax2+bx+c的图象过点C（t，2），
∴at2+bt+c=2
∵AC⊥BC，
∴
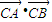=（x1-t，-2）•（x2-t，-2）=0
∴
∴
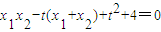
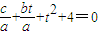
即at2+bt+c+4a=0
∴4a+2=0
∴
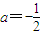
故答案为：-
点评：本题主要考查了利用二次函数的性质求解函数中的参数，解题中注意整体思想的应用．
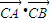=（x1-t，-2）•（x2-t，-2）=0，代入根据方程的根与系数关系可求a解答：解：设A（x1，0），B（x2，0）
∵二次函数y=ax2+bx+c的图象过点C（t，2），
∴at2+bt+c=2
∵AC⊥BC，
∴
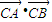=（x1-t，-2）•（x2-t，-2）=0∴
∴
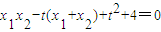
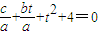
即at2+bt+c+4a=0
∴4a+2=0
∴
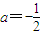
故答案为：-
点评：本题主要考查了利用二次函数的性质求解函数中的参数，解题中注意整体思想的应用．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
如图，已知二次函数y=x2-2x-1的图象的顶点为A．二次函数y=ax2+bx的图象与x轴交于原点O及另一点C，它的顶点B在函数y=x2-2x-1的图象的对称轴上．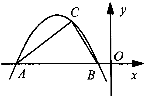
如图，已知二次函数y=ax2+bx+c（a，b，c为实数，a≠0）的图象过点C（t，2），且与x轴交于A，B两点，若AC⊥BC，则a的值为
