题目内容
已知△ABC的内角A,B,C的对边分别为a,b,c,其中c=2,又向量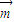 =(1,cosC),
=(1,cosC),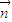 =(cosC,1),
=(cosC,1),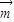 •
•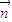 =1.
=1.(1)若A=45°,求a的值;
(2)若a+b=4,求△ABC的面积.
【答案】分析:(1)根据平面向量的数量积运算化简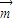 •
•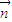 =1,得到cosC的值,根据C的范围和特殊角的三角函数值求出C的度数,然后利用正弦定理,由c和A的值求出a的值即可;
=1,得到cosC的值,根据C的范围和特殊角的三角函数值求出C的度数,然后利用正弦定理,由c和A的值求出a的值即可;
(2)根据c和cosC的值,利用余弦定理表示出一个关于a与b的关系式,由a+b的值求出ab的值,然后利用三角形的面积公式即可求出△ABC的面积.
解答:解:(1)∵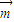 •
•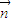 =cosC+cosC=2cosC=1,
=cosC+cosC=2cosC=1,
∴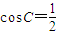 ,
,
∵0°<C<180°,
∴C=60°,
由正弦定理得,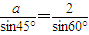 ,
,
∴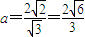 ;
;
(2)∵c=2,∠C=60°∴a2+b2-2abcos60°=4,
∴a2+b2-ab=4,
又∵a+b=4,∴a2+b2+2ab=16,∴ab=4,
∴S△ABC= absinC=
absinC=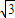 .
.
点评:此题要求学生掌握平面向量的数量积的运算法则,利用运用正弦、余弦定理及三角形的面积公式化简求值,是一道多知识的综合题.
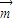 •
•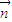 =1,得到cosC的值,根据C的范围和特殊角的三角函数值求出C的度数,然后利用正弦定理,由c和A的值求出a的值即可;
=1,得到cosC的值,根据C的范围和特殊角的三角函数值求出C的度数,然后利用正弦定理,由c和A的值求出a的值即可;(2)根据c和cosC的值,利用余弦定理表示出一个关于a与b的关系式,由a+b的值求出ab的值,然后利用三角形的面积公式即可求出△ABC的面积.
解答:解:(1)∵
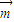 •
•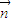 =cosC+cosC=2cosC=1,
=cosC+cosC=2cosC=1,∴
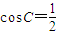 ,
,∵0°<C<180°,
∴C=60°,
由正弦定理得,
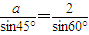 ,
,∴
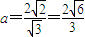 ;
;(2)∵c=2,∠C=60°∴a2+b2-2abcos60°=4,
∴a2+b2-ab=4,
又∵a+b=4,∴a2+b2+2ab=16,∴ab=4,
∴S△ABC=
 absinC=
absinC=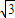 .
.点评:此题要求学生掌握平面向量的数量积的运算法则,利用运用正弦、余弦定理及三角形的面积公式化简求值,是一道多知识的综合题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目