Question

如图，圆形花坛水池中央有一喷泉，水管OP=1m，水从喷头P喷出后呈抛物线状，先向上至最高点后落下，若最高点距水面2m，P距抛物线对称轴1m，则为使水不落到池外，水池直径最小为______m．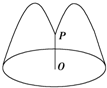

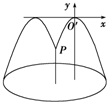
Answer 1

如图，建立平面直角坐标系，设抛物线方程为x²=-2py（p＞0），
则P（-1，-1），代入抛物线方程得p=

1

2

，抛物线x²=-y，代点（x，-2），
得x=

2

，即水池半径最小为r=（1+

2

）m，
水池直径最小为2r=（2+2

2

）m．
故答案为：2+2

2

．