题目内容
已知实轴长为2a,虚轴长为2b的双曲线S的焦点在x轴上,直线y=+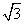 x是双曲线S的一条渐近线,而且原点O,点A(a,0)和点B(0,-b)使等式
x是双曲线S的一条渐近线,而且原点O,点A(a,0)和点B(0,-b)使等式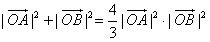 成立,
成立,
(Ⅰ)求双曲线S的方程;
(Ⅱ)若双曲线S上存在两个点关于直线l:y=kx+4对称,求实数k的取值范围。
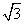 x是双曲线S的一条渐近线,而且原点O,点A(a,0)和点B(0,-b)使等式
x是双曲线S的一条渐近线,而且原点O,点A(a,0)和点B(0,-b)使等式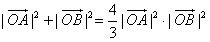 成立,
成立, (Ⅰ)求双曲线S的方程;
(Ⅱ)若双曲线S上存在两个点关于直线l:y=kx+4对称,求实数k的取值范围。
解:(Ⅰ)根据题意设双曲线S的方程为 ,
,
且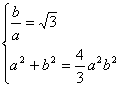 ,解方程组得
,解方程组得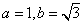 ,
,
∴所求双曲线的方程为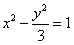 。
。
(Ⅱ)当k=0时,双曲线S上显然不存在两个点关于直线l:y=kx+4对称;
当k≠0时,设又曲线S上的两点M、N关于直线l对称,
由l⊥MN,直线MN的方程为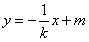 ,
,
则M、N两点的坐标满足方程组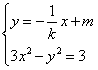 ,
,
消去y得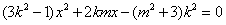 ,
,
显然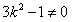 ,
,
∴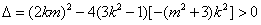 ,
,
即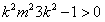 ,
,
设线段MN中点为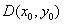 ,
,
则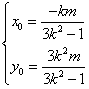 ,
,
∵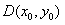 在直线l:y=kx+4上,
在直线l:y=kx+4上,
∴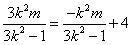 ,即
,即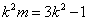 ,
,
∴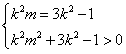 ,∴
,∴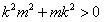 ,解得m>0或m<-1,
,解得m>0或m<-1,
∴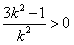 或
或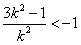 ,
,
∴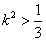 或
或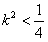 ,即
,即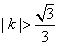 或
或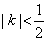 ,且k≠0,
,且k≠0,
∴k的取值范围是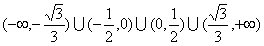 。
。
 ,
,且
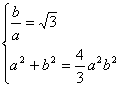 ,解方程组得
,解方程组得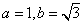 ,
,∴所求双曲线的方程为
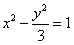 。
。 (Ⅱ)当k=0时,双曲线S上显然不存在两个点关于直线l:y=kx+4对称;
当k≠0时,设又曲线S上的两点M、N关于直线l对称,
由l⊥MN,直线MN的方程为
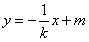 ,
,则M、N两点的坐标满足方程组
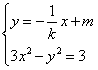 ,
,消去y得
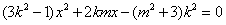 ,
,显然
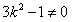 ,
,∴
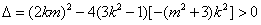 ,
,即
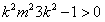 ,
,设线段MN中点为
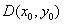 ,
,则
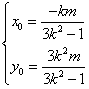 ,
,∵
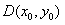 在直线l:y=kx+4上,
在直线l:y=kx+4上,∴
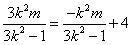 ,即
,即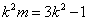 ,
,∴
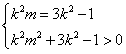 ,∴
,∴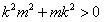 ,解得m>0或m<-1,
,解得m>0或m<-1,∴
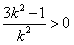 或
或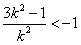 ,
,∴
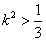 或
或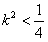 ,即
,即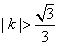 或
或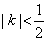 ,且k≠0,
,且k≠0,∴k的取值范围是
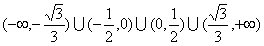 。
。
练习册系列答案
相关题目
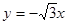 是双曲线S的一条渐近线,而且原点O,点A(a,0)和点B(0,-b)使等式
是双曲线S的一条渐近线,而且原点O,点A(a,0)和点B(0,-b)使等式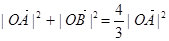 ·
·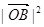 成立.
成立.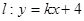 对称,求实数k的取值范围.
对称,求实数k的取值范围.