题目内容
已知x∈R,函数f(x)=2sin
+3cos
的最小正周期为
| x |
| 2 |
| x |
| 3 |
12π
12π
.分析:求出两个函数的周期,然后求出它们的最小公倍数,即可确定函数的周期.
解答:解:因为函数y=sin
的周期为:
=4π,函数y=cos
的周期为:
=6π;
4π与6π的最小公倍数是12π,
所以函数f(x)=2sin
+3cos
的最小正周期为:12π.
故答案为:12π.
| x |
| 2 |
| 2π | ||
|
| x |
| 3 |
| 2π | ||
|
4π与6π的最小公倍数是12π,
所以函数f(x)=2sin
| x |
| 2 |
| x |
| 3 |
故答案为:12π.
点评:本题是基础题,考查函数的周期的求法,一般情况化简为一个函数求解,本题的方法是求出周期的最小公倍数.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
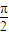 ,π),
,π),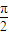 ,π),
,π),