题目内容
已知x∈R,函数f(x)=ax3+bx2+cx+d在x=0处取得极值,曲线y=f(x)过原点O(0,0)和点P(-1,2).若曲线y=f(x)在点P处的切线l与直线y=2x的夹角为45°,且直线l的倾斜角θ∈(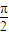 ,π),
,π),(Ⅰ)求f(x)的解析式;
(Ⅱ)若函数y=f(x)在区间[2m-1,m+1]上是增函数,求实数m的取值范围;
(Ⅲ)若x1、x2∈[-1,1],求证:f(x1)-f(x2)≤4.
【答案】分析:(I)根据在x=0处取得极值以及过点(0,0)可求出c和d,然后根据曲线y=f(x)在点P处的切线l与直线y=2x的夹角为45°,建立方程求出a和b,从而求出函数的解析式;
(II)令f'(x)>0求出函数f(x)的增区间,使[2m-1,m+1]是增区间的子集,建立不等关系,解之即可;
(III)先利用导数求出函数f(x)在[-1,1]上的最大值和最小值,f(x1)-f(x2)≤f(x)max-f(x)min,从而得到结论.
解答:解(Ⅰ)由已知f'(x)=3ax2+2bx+c∴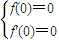 ⇒c=d=0∴c=d=0…(2分)
⇒c=d=0∴c=d=0…(2分)
又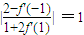 且f'(-1)<0∴f'(-1)=-3 (舍去f'(-1)=
且f'(-1)<0∴f'(-1)=-3 (舍去f'(-1)= )
)
∴ ⇒
⇒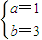 ⇒f(x)=x3+3x2…(4分)
⇒f(x)=x3+3x2…(4分)
(Ⅱ)令f'(x)=3x(x+2)>0⇒x>0或x<-2 即f(x)的增区间为(-∞,-2]、[0,+∞)
∵y=f(x)在区间[2m-1,m+1]上是增函数
∴2m-1<m+1≤-2或0≤2m-1<m+1 则m≤-3或 ≤m<2…(8分)
≤m<2…(8分)
(Ⅲ)令f'(x)=3x(x+2)=0⇒x=0或x=-2
∵f(0)=0,f(-1)=2,f(1)=4∴y=f(x)在[-1,1]上的最大值为4,最小值为0…(10分)
∴x1、x2∈[-1,1]时,|f(x1)-f(x2)|≤4-0=4…(12分)
点评:本题主要考查函数解析式,函数单调性和不等式的证明,从已知条件出发,利用定义、公理、定理、某些已经证明过的不等式及不等式的性质经过一系列的推理、论证等而推导出所要证明的不等式.
(II)令f'(x)>0求出函数f(x)的增区间,使[2m-1,m+1]是增区间的子集,建立不等关系,解之即可;
(III)先利用导数求出函数f(x)在[-1,1]上的最大值和最小值,f(x1)-f(x2)≤f(x)max-f(x)min,从而得到结论.
解答:解(Ⅰ)由已知f'(x)=3ax2+2bx+c∴
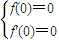 ⇒c=d=0∴c=d=0…(2分)
⇒c=d=0∴c=d=0…(2分)又
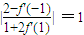 且f'(-1)<0∴f'(-1)=-3 (舍去f'(-1)=
且f'(-1)<0∴f'(-1)=-3 (舍去f'(-1)= )
)∴
 ⇒
⇒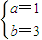 ⇒f(x)=x3+3x2…(4分)
⇒f(x)=x3+3x2…(4分)(Ⅱ)令f'(x)=3x(x+2)>0⇒x>0或x<-2 即f(x)的增区间为(-∞,-2]、[0,+∞)
∵y=f(x)在区间[2m-1,m+1]上是增函数
∴2m-1<m+1≤-2或0≤2m-1<m+1 则m≤-3或
 ≤m<2…(8分)
≤m<2…(8分)(Ⅲ)令f'(x)=3x(x+2)=0⇒x=0或x=-2
∵f(0)=0,f(-1)=2,f(1)=4∴y=f(x)在[-1,1]上的最大值为4,最小值为0…(10分)
∴x1、x2∈[-1,1]时,|f(x1)-f(x2)|≤4-0=4…(12分)
点评:本题主要考查函数解析式,函数单调性和不等式的证明,从已知条件出发,利用定义、公理、定理、某些已经证明过的不等式及不等式的性质经过一系列的推理、论证等而推导出所要证明的不等式.

练习册系列答案
相关题目
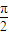 ,π),
,π),