题目内容
方程sinx=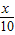 的根的个数为( )
的根的个数为( )A.7
B.8
C.9
D.10
【答案】分析:方程sinx=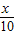 的根的个数即为函数y=sinx 与 直线y=
的根的个数即为函数y=sinx 与 直线y=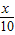 的交点的个数,
的交点的个数,
在(0,10)上有3个交点,在(-10,0)上也有3个交点,在原点有一个交点.
解答:解:方程sinx=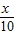 的根的个数即为函数y=sinx 与 直线y=
的根的个数即为函数y=sinx 与 直线y=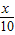 的交点的个数,
的交点的个数,
直线y= 过原点,在(0,10)上和函数y=sinx 有3个交点,在(-10,0)上也有3个交点,
过原点,在(0,10)上和函数y=sinx 有3个交点,在(-10,0)上也有3个交点,
在原点和函数y=sinx 有一个交点,在其它的区间上,这两个函数没有交点,
故这两个函数的交点个数为7,即方程sinx=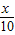 的根的个数 为7,
的根的个数 为7,
故选 A.
点评:本题考查方程的根与两个函数的交点的关系,体现了转化的数学思想.
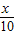 的根的个数即为函数y=sinx 与 直线y=
的根的个数即为函数y=sinx 与 直线y=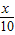 的交点的个数,
的交点的个数,在(0,10)上有3个交点,在(-10,0)上也有3个交点,在原点有一个交点.
解答:解:方程sinx=
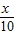 的根的个数即为函数y=sinx 与 直线y=
的根的个数即为函数y=sinx 与 直线y=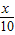 的交点的个数,
的交点的个数,直线y=
 过原点,在(0,10)上和函数y=sinx 有3个交点,在(-10,0)上也有3个交点,
过原点,在(0,10)上和函数y=sinx 有3个交点,在(-10,0)上也有3个交点,在原点和函数y=sinx 有一个交点,在其它的区间上,这两个函数没有交点,
故这两个函数的交点个数为7,即方程sinx=
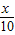 的根的个数 为7,
的根的个数 为7,故选 A.
点评:本题考查方程的根与两个函数的交点的关系,体现了转化的数学思想.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 的根的个数为
的根的个数为