题目内容
(08年福建卷理)(本小题满分14分)
已知函数![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)记![]() 在区间
在区间![]() (n∈N*)上的最小值为
(n∈N*)上的最小值为![]() ,令
,令![]() .
.
① 如果对一切n,不等式![]() 恒成立,求实数c的取值范围;
恒成立,求实数c的取值范围;
() 求证:![]() .
.
解析:解法一:
(I)因为![]() ,所以函数定义域为
,所以函数定义域为![]() ,且
,且![]() 。
。
由![]() 得
得![]() ,
,![]() 的单调递增区间为
的单调递增区间为![]() ;
;
由![]() <0得
<0得![]() ,
,![]() 的单调递增区间为(0,+
的单调递增区间为(0,+![]() ).
).
(Ⅱ)因为![]() 在
在![]() 上是减函数,所以
上是减函数,所以![]() ,
,
则![]() .
.
()![]()
![]()
又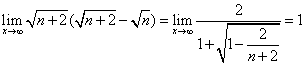 ,
,
因此![]() ,即实数c的取值范围是
,即实数c的取值范围是![]() .
.
() 由①知![]()
因为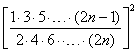
![]()
所以![]() <
<![]()
![]() ,
,
则![]()
![]()
![]() .
.
解法二:
(I)同解法一。
(Ⅱ)因为![]() 在
在![]() 上是减函数,所以
上是减函数,所以![]() ,
,
则![]() .
.
() 因为![]() 对
对![]() 恒成立,
恒成立,
所以![]() 对
对![]() 恒成立。
恒成立。
则![]() 对
对![]() 恒成立。
恒成立。
设![]() ,
,![]() ,则
,则![]() 对
对![]() 恒成立。
恒成立。
考虑![]() 。
。
因为![]()
![]() 在
在![]() 内是减函数;则当
内是减函数;则当![]() 时,
时,![]() 随
随![]() 的增大而减小。
的增大而减小。
又因为![]()
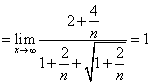 。
。
所以对一切![]() ,
,![]() 。因此
。因此![]() ,即实数c的取值范围是
,即实数c的取值范围是![]() .
.
() 由()知![]()
下面用数学归纳法证明不等式
![]()
![]() ,
,
① 当![]() 时,左边
时,左边![]() ,右边
,右边![]() ,左边
,左边![]() 右边,不等式成立。
右边,不等式成立。
② 假设当![]() 时,不等式成立.即
时,不等式成立.即![]() 。
。
当![]() 时,
时,
![]()
![]()
![]() 。
。
即![]() 时,不等式成立.
时,不等式成立.
综合①、②得,![]()
![]() 成立。
成立。
所以![]()
![]()
![]()
![]() 。
。
![]() .
.
【高考考点】本小题主要考查函数的单调性、最值、不等式、数列等基本知识,考查运用导数研究函数性质的方法,考查分析问题和解决问题的能力,满分14分.
【易错提醒】第一问中导数记不住公式
【备考提示】此题为压轴题,所以平时可以让学生学会放弃一些自己能力范围之外的题目,把多余的时间多花点在中低档题目上,可是80%的分数呀,多么可观,可是纵观历年的高考成绩来看又有多少人真正的做到了这120分?

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目