��Ŀ����
��֪����{an}�У�a1=1���ҵ�P��an��an+1����ֱ��x-y+1=0�ϡ�
��1��������{an}��ͨ�ʽ��
��2��������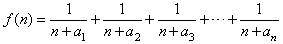 ��n��N����n��2��������f��n������Сֵ��
��n��N����n��2��������f��n������Сֵ��
��3����bn=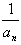 ��Sn��ʾ����{bn}��ǰn��͡����ʣ��Ƿ���ڹ���n����ʽg��n����ʹ��S1+S2+S3+��+Sn-1=��Sn-1����g��n������һ�в�С��2����Ȼ��n������� �����ڣ�д��g��n���Ľ���ʽ��������֤�����������ڣ���˵�����ɡ�
��Sn��ʾ����{bn}��ǰn��͡����ʣ��Ƿ���ڹ���n����ʽg��n����ʹ��S1+S2+S3+��+Sn-1=��Sn-1����g��n������һ�в�С��2����Ȼ��n������� �����ڣ�д��g��n���Ľ���ʽ��������֤�����������ڣ���˵�����ɡ�
�⣺��1���ɵ�P��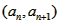 ֱ��x-y+1=0�ϣ���
ֱ��x-y+1=0�ϣ���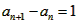 ����
���� ������{
������{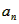 }����1Ϊ���1Ϊ����ĵȲ�����
}����1Ϊ���1Ϊ����ĵȲ����� ��
��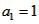 ͬ�����㣬����
ͬ�����㣬����
��2��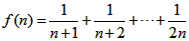
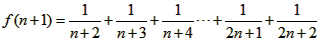

����f��n���ǵ�����������f��n������Сֵ��f��2��=
��3��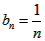 ���ɵ�
���ɵ�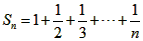 ��
��
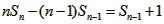
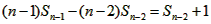
����
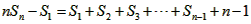
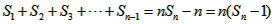 ��n��2 ��
��n��2 ��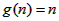
�ʴ��ڹ���n����ʽg��x��=n,ʹ�ö���һ�в�С��2����Ȼ��n�������

��ϰ��ϵ�д�
 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
�����Ŀ
��֪����{an}�У�a1=1��2nan+1=��n+1��an��������{an}��ͨ�ʽΪ��������
A��
| ||
B��
| ||
C��
| ||
D��
|