题目内容
若A={2,4,x3-2x2-x+7},B={1,x+1,x2-2x+2,![]() (x2-3x-8),x3+x2+3x+7},若A∩B={2,5},求实数x的值.
(x2-3x-8),x3+x2+3x+7},若A∩B={2,5},求实数x的值.
答案:
解析:
提示:
解析:
|
解:∵A∩B={2,5},∴5∈A. ∴x3-2x2-x+7=5,解得x=2,或x=±1. 当x=2时,A={2,4,5},B={1,3,2,5,25},则x=2满足题意. 当x=1时,B中x2-2x+2=1,不符合集合元素的互异性,故x=1舍去. 当x=-1时,B={1,0,5,2,4},此时A∩B={2,4,5}不合题意,故x=-1舍去. 综上所得,x=2. |
提示:
|
解决本题的关键是对A∩B={2,5}的理解,由集合的运算性质得(A∩B) |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 x3-
x3- x2+ax.
x2+ax. .
.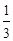 x3-
x3-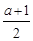 x2+ax.
x2+ax. .
.