题目内容

11．已知（1+2i） z=3-i（i为虚数单位），则复数z=$\frac{1}{5}-\frac{7}{5}i$．

分析 直接由复数代数形式的除法运算化简求值即可得答案．

解答 解：由（1+2i） z=3-i，
得$z=\frac{3-i}{1+2i}=\frac{（3-i）（1-2i）}{（1+2i）（1-2i）}=\frac{1-7i}{5}=\frac{1}{5}-\frac{7}{5}i$．
故答案为：$\frac{1}{5}-\frac{7}{5}i$．

点评 本题考查了复数代数形式的乘除运算，考查了复数的基本概念，是基础题．

练习册系列答案
相关题目
1．执行如图所示的算法流程图．若输入x=0，则输出的y的值是（　　）
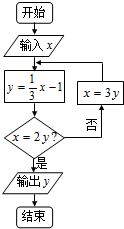
A．-3B．-2C．-1D．0
2．已知函数f（x）=cos（ωx+φ）（ω＞0，π＜φ＜2π）为奇函数，且图象上相邻的一个最高点和一个最低点之间的距离为$\sqrt{4+{π}^{2}}$．
（1）求函数f（x）的解析式；
（2）若f（α）=$\frac{3}{5}$，α为第二象限角，求tan（α-$\frac{π}{4}$）的值．
19．已知x，y满足约束条件$\left\{\begin{array}{l}{x+y-1≥0}\\{x+2y-2≤0}\\{kx-y-2k≤0}\end{array}\right.$，其中k＞0，若z=$\frac{1}{3}$x+y的最小值为0，则k=1．
6．已知函数f（x）=$\frac{1-x}{{1+a{x^2}}}$，其中a∈R．
（Ⅰ）当a=-$\frac{1}{4}$时，求函数f（x）的图象在点（1，f（1））处的切线方程；
（Ⅱ）当a＞0时，证明：存在实数m＞0，使得对任意的x，都有-m≤f（x）≤m成立；
（Ⅲ）当a=2时，是否存在实数k，使得关于x的方程f（x）=k（x-a）仅有负实数解？当a=-$\frac{1}{2}$时的情形又如何？（只需写出结论）
16．已知集合M={0，1}，N={-1，0}，则M∩N=（　　）
A．{-1，0，1}B．{-1，1}C．{0}D．φ
3．直线y=-2x+2恰好经过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的右焦点和上顶点，则椭圆的离心率等于（　　）
A．$\frac{\sqrt{5}}{5}$B．$\frac{1}{2}$C．$\frac{2\sqrt{5}}{5}$D．$\frac{\sqrt{5}}{2}$
1．已知：求所有实数k，使得存在△ABC，满足
（1）a+b=kc；
（2）cot$\frac{A}{2}$+cot$\frac{B}{2}$=kcot$\frac{C}{2}$．
2．已知函数f（x）=ae-x-x+1，a∈R．
（Ⅰ）当a=1时，求曲线y=f（x）在（0，f（0））处的切线方程；
（Ⅱ）若对任意x∈（0，+∞），f（x）＜0恒成立，求a的取值范围；
（Ⅲ）当x∈（0，+∞）时，求证：2e-x-2＜$\frac{1}{2}$x2-x．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网