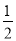题目内容
2. 如图,在平面直角坐标系xOy中,点A(8,-4),P(2,t)(t<0)在抛物线y2=2px(p>0)上.
如图,在平面直角坐标系xOy中,点A(8,-4),P(2,t)(t<0)在抛物线y2=2px(p>0)上.(1)求p,t的值;
(2)过点P作PM垂直于x轴,M为垂足,直线AM与抛物线的另一交点为B,点C在直线AM上.若PA,PB,PC的斜率分别为k1,k2,k3,且k1+k2=2k3,求点C的坐标.
分析 (1)运用代入法,即可求得p,t;
(2)求得M(2,0),求出直线AM的方程,代入抛物线方程,可得B的坐标,运用正弦的斜率公式,可得k1=-$\frac{1}{3}$,k2=-2,代入k1+k2=2k3得k3,进而得到直线PC方程,再联立直线AM的方程,即可得到C的坐标.
解答 解:(1)将点A(8,-4)代入y2=2px,
得p=1,
将点P(2,t)代入y2=2x,得t=±2,
因为t<0,所以t=-2.
(2)依题意,M的坐标为(2,0),
直线AM的方程为y=-$\frac{2}{3}$x+$\frac{4}{3}$,
联立抛物线方程y2=2x,并解得B($\frac{1}{2}$,1),
所以k1=-$\frac{1}{3}$,k2=-2,
代入k1+k2=2k3得,k3=-$\frac{7}{6}$,
从而直线PC的方程为y=-$\frac{7}{6}$x+$\frac{1}{3}$,
联立直线AM:y=-$\frac{2}{3}$x+$\frac{4}{3}$,
并解得C(-2,$\frac{8}{3}$).
点评 本题考查抛物线的方程和性质,主要考查方程的运用,注意联立直线方程和抛物线方程求交点,以及直线的斜率公式的运用和两直线的交点问题转化为解方程,属于中档题.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
17.在平面直角坐标系中,直线y=$\frac{\sqrt{3}}{3}$x与圆x2+y2-8x+4=0交于A、B两点,则线段AB的长为( )
| A. | 4$\sqrt{2}$ | B. | 4$\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
7. 函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2015)的值为( )
函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2015)的值为( )
 函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2015)的值为( )
函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2015)的值为( )| A. | 0 | B. | 3$\sqrt{2}$ | C. | 6$\sqrt{2}$ | D. | -$\sqrt{2}$ |
14.若集合A={1,m,m2},集合B={2,4},则“m=-2”是“A∩B={4}”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
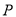 是
是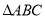 所在平面内一点且
所在平面内一点且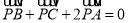 ,现将一粒黄豆随机撕在
,现将一粒黄豆随机撕在 内的概率是( )
内的概率是( )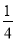 B.
B.
 D.
D.