题目内容
已知圆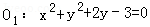 内一定点A(1,﹣2),P,Q为圆上的两不同动点.
内一定点A(1,﹣2),P,Q为圆上的两不同动点.
(1)若P,Q两点关于过定点A的直线l对称,求直线l的方程;
(2)若圆O2的圆心O2与点A关于直线x+3y=0对称,圆O2与圆O1交于M,N两点,且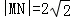 ,求圆O2的方程.
,求圆O2的方程.
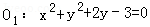 内一定点A(1,﹣2),P,Q为圆上的两不同动点.
内一定点A(1,﹣2),P,Q为圆上的两不同动点.(1)若P,Q两点关于过定点A的直线l对称,求直线l的方程;
(2)若圆O2的圆心O2与点A关于直线x+3y=0对称,圆O2与圆O1交于M,N两点,且
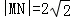 ,求圆O2的方程.
,求圆O2的方程.解:(1)将圆O1的方程化为标准方程得:x2+(y+1)2=4,
∴O1(0,﹣1),又P,Q两点关于过定点A的直线l对称,
∴O1(0,﹣1)在直线l上,又直线l过A(1,﹣2),
∴直线l的方程为y+2=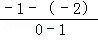 (x﹣1),即x+y+1=0;
(x﹣1),即x+y+1=0;
(2)设O2(a,b),
∵O2与A关于直线x+3y=0对称,且x+3y=0的斜率为﹣ ,
,
∴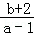 =3①,且
=3①,且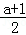 +3×
+3×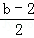 =0②,
=0②,
联立①②解得:a=2,b=1,∴O2(2,1),
可设圆O2的方程为:(x﹣2)2+(y+1)2=r2,
又圆O1的方程为:x2+(y+1)2=4,
∴两圆方程相减,即得两圆公共弦MN所在直线的方程为4x+4y+r2﹣8=0,
∵|MN|=2 ,圆O1的半径为2,
,圆O1的半径为2,
∴O1到直线MN的距离为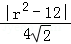 =
= =
=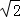 ,
,
解得:r2=20或r2=4,
则圆O2的方程为:(x﹣2)2+(y+1)2=20或(x﹣2)2+(y+1)2=4.
∴O1(0,﹣1),又P,Q两点关于过定点A的直线l对称,
∴O1(0,﹣1)在直线l上,又直线l过A(1,﹣2),
∴直线l的方程为y+2=
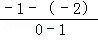 (x﹣1),即x+y+1=0;
(x﹣1),即x+y+1=0;(2)设O2(a,b),
∵O2与A关于直线x+3y=0对称,且x+3y=0的斜率为﹣
 ,
,∴
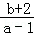 =3①,且
=3①,且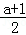 +3×
+3×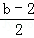 =0②,
=0②,联立①②解得:a=2,b=1,∴O2(2,1),
可设圆O2的方程为:(x﹣2)2+(y+1)2=r2,
又圆O1的方程为:x2+(y+1)2=4,
∴两圆方程相减,即得两圆公共弦MN所在直线的方程为4x+4y+r2﹣8=0,
∵|MN|=2
 ,圆O1的半径为2,
,圆O1的半径为2,∴O1到直线MN的距离为
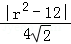 =
= =
=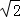 ,
,解得:r2=20或r2=4,
则圆O2的方程为:(x﹣2)2+(y+1)2=20或(x﹣2)2+(y+1)2=4.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 内一定点A(1,-2),P,Q为圆上的两不同动点.
内一定点A(1,-2),P,Q为圆上的两不同动点. ,求圆O2的方程.
,求圆O2的方程. 内一定点A(1,-2),P,Q为圆上的两不同动点.
内一定点A(1,-2),P,Q为圆上的两不同动点. ,求圆O2的方程.
,求圆O2的方程.