题目内容
已知动圆P与定圆B:x2+y2+2x-35=0内切,且动圆经过一定点A(1,0).(1)求动圆圆心P的轨迹方程;
(2)过点B(圆心)的直线与点P的轨迹交与M,N两点,求△AMN面积的最大值.
分析:(1)定圆B的圆心为B(-1,0),半径r=6,因为动圆P与定圆B内切,且动圆P过定点A(1,0),所以|PA|+|PB|=6.由此能求出椭圆的方程.
(2)由题意设直线l的方程为my=x+1,与点P的轨迹方程
+
=1联立,得(8m2+9)y2-16my-64=0,设M(x1,y1),N(x2,y2),则y1+y2=
,y1y2=-
,S△AMN=
×2c×|y1-y2|=
,由此能求出△AMN面积的最大值.
(2)由题意设直线l的方程为my=x+1,与点P的轨迹方程
| x2 |
| 9 |
| y2 |
| 8 |
| 16m |
| 8m2+9 |
| 64 |
| 8m2+9 |
| 1 |
| 2 |
48
| ||
| 8m2+9 |
解答:解:(1)定圆B的圆心为B(-1,0),半径r=6,
因为动圆P与定圆B内切,且动圆P过定点A(1,0)
所以|PA|+|PB|=6.
所以动圆圆心P的轨迹是以B、A为焦点,长轴长为6的椭圆.
∴所求椭圆的方程为
+
=1.(5分)
(2)由题意设直线l的方程为my=x+1,
与点P的轨迹方程
+
=1联立,得(8m2+9)y2-16my-64=0,
设M(x1,y1),N(x2,y2),
则y1+y2=
,y1y2=-
,
∴S△AMN=
×2c×|y1-y2|=
,
令
=t>1,则m2=t2-1,
∴S△AMN=
=
,
∵8t+
在[1,+∞)上单调递增,
∴8t+
≥9(当且仅当t=1时取”=”),
∴△AMN面积的最大值为
.
因为动圆P与定圆B内切,且动圆P过定点A(1,0)
所以|PA|+|PB|=6.
所以动圆圆心P的轨迹是以B、A为焦点,长轴长为6的椭圆.
∴所求椭圆的方程为
| x2 |
| 9 |
| y2 |
| 8 |
(2)由题意设直线l的方程为my=x+1,
与点P的轨迹方程
| x2 |
| 9 |
| y2 |
| 8 |
设M(x1,y1),N(x2,y2),
则y1+y2=
| 16m |
| 8m2+9 |
| 64 |
| 8m2+9 |
∴S△AMN=
| 1 |
| 2 |
48
| ||
| 8m2+9 |
令
| m2+1 |
∴S△AMN=
| 48t |
| 8t2+1 |
| 48 | ||
8t+
|
∵8t+
| 1 |
| t |
∴8t+
| 1 |
| t |
∴△AMN面积的最大值为
| 48 |
| 9 |
点评:本题考查椭圆方程的求法和三角形面积最大值的计算,解题时要认真审题,注意合理地进行等价转化.

练习册系列答案
相关题目
 内切,且动圆P经过一定点A(
内切,且动圆P经过一定点A( ,0).
,0).
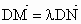 ,求实数λ的取值范围.
,求实数λ的取值范围.