题目内容
【题目】抛物线y2=﹣12x的准线与双曲线 
﹣ 
=1的两条渐近线所围成的三角形的面积等于 ．
【答案】
【解析】解：∵抛物线方程为y2=﹣12x，
∴抛物线的焦点为F（﹣3，0），准线为x=3．
又∵双曲线 
﹣ 
=1的渐近线方程为y=± 
x．
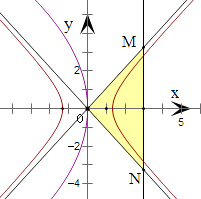
∵直线x=3与直线y=± x相交于点M（3， 
），N（3，﹣），
∴三条直线围成的三角形为△MON，以MN为底边、O到MN的距离为高，
可得其面积为S= 
×|MN|×3= ×[ ﹣（﹣ ）]×3=3 ．
故答案为： 
．
根据抛物线的方程算出其准线方程为x=3，由双曲线的方程算出渐近线方程为y=± x，从而得到它们的交点M、N的坐标，再利用三角形的面积公式算出△OMN的面积，可得答案．
练习册系列答案
相关题目
