Question

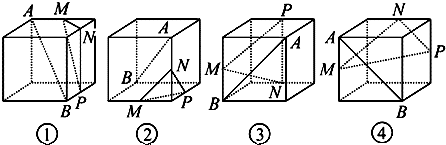
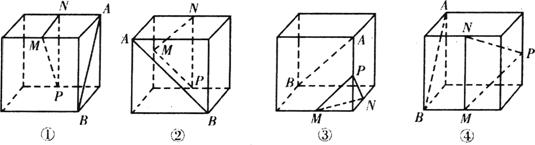
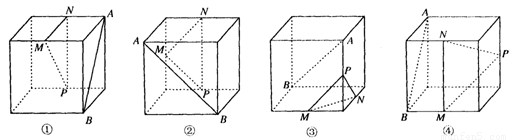
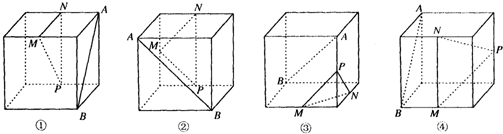
下面四个正方体图形中，A、B为正方体的两个顶点，M、N、P分别为其所在棱的中点，能得出AB∥平面MNP的图形是（　　）

A．①②

B．①④

C．②③

D．③④

Answer 1

分析：①如图所示，取棱BC的中点Q，连接MQ，PQ，NQ，可得四边形MNPQ为正方形，利用正方形的性质可得AB∥NQ，利用线面平行判定定理可得AB∥平面MNPQ．
②由正方体可得：前后两个侧面平行，利用面面平行的性质可得AB∥MNP．

解答：解：①如图所示，取棱BC的中点Q，连接MQ，PQ，NQ，可得四边形MNPQ为正方形，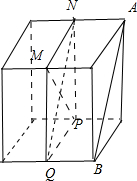
且AB∥NQ，而NQ?平面MNPQ，AB?平面MNPQ，∴AB∥平面MNPQ，因此正确．
②由正方体可得：前后两个侧面平行，因此AB∥MNP，因此正确．
故选A．

点评：熟练掌握正方体的性质及线面、面面平行的判定与性质定理是解题的关键．