题目内容
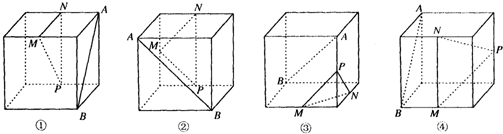
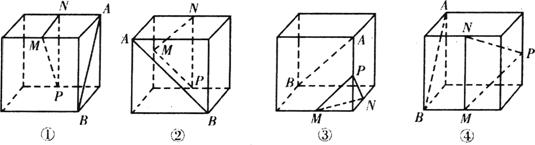
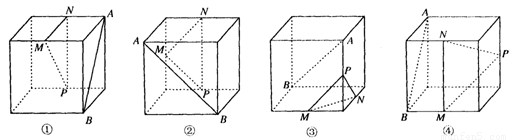
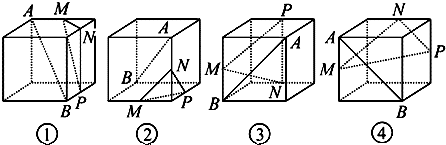
下面四个正方体图形中，A、B为正方体的两个顶点，M、N、P分别为其所在棱的中点，能得出AB∥平面MNP的图形是
①④
①④
分析：分别根据平面MNP的位置确定直线AB是否与平面平行．
解答：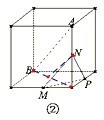
解：①连结BC，则平面ABC∥平面MNP，所以AB∥平面MNP．所以①正确．
②取底面正方形对角线的中点O，则ON∥AB，所以AB与面PMN相交，不平行，所以②不合适．
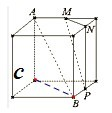
③AB与面PMN相交，不平行，所以③不合适．
④因为AB∥NP，所以AB∥平面MNP．所以④正确．
故答案为：①④．
解：①连结BC，则平面ABC∥平面MNP，所以AB∥平面MNP．所以①正确．②取底面正方形对角线的中点O，则ON∥AB，所以AB与面PMN相交，不平行，所以②不合适．
③AB与面PMN相交，不平行，所以③不合适．
④因为AB∥NP，所以AB∥平面MNP．所以④正确．
故答案为：①④．
点评：本题主要考查线面平行的判定，利用线面平行的判定，只要直线AB平行于平面MNP内的一条直线即可．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
