题目内容
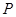 为椭圆
为椭圆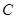 上一点,
上一点,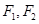 为两焦点,
为两焦点,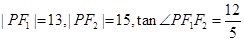 ,则椭圆
,则椭圆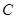 的离心率
的离心率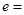 .
.
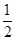
解析试题分析: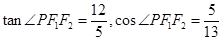 ,由余弦定理得
,由余弦定理得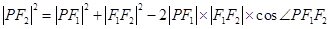 ,
,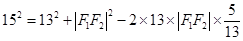 ,所以
,所以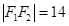 ,又
,又 ,所以椭圆
,所以椭圆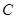 的离心率
的离心率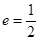 .
.
考点:椭圆的定义,余弦定理.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
题目内容
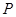 为椭圆
为椭圆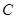 上一点,
上一点,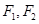 为两焦点,
为两焦点,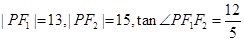 ,则椭圆
,则椭圆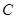 的离心率
的离心率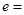 .
.
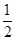
解析试题分析: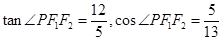 ,由余弦定理得
,由余弦定理得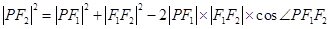 ,
,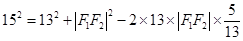 ,所以
,所以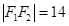 ,又
,又 ,所以椭圆
,所以椭圆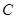 的离心率
的离心率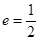 .
.
考点:椭圆的定义,余弦定理.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案