题目内容
12.已知x+x-1=2,求$\frac{{x}^{2}+{x}^{-2}-2}{{x}^{\frac{3}{2}}+{x}^{-\frac{3}{2}}-3}$.分析 由x+x-1=2,可得x2+x-2=(x+x-1)2-2=2,代入即可得出.
解答 解:∵x+x-1=2,∴x2+x-2=(x+x-1)2-2=2,
∴$\frac{{x}^{2}+{x}^{-2}-2}{{x}^{\frac{3}{2}}+{x}^{-\frac{3}{2}}-3}$=0.
点评 本题考查了指数幂的运算性质、乘法公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
4.在平面直角坐标系中,过动点P分别作圆C1:x2+y2-4x-6y+9=0与圆C2:x2+y2+2x+2y+1=0的切线PA与PB(A,B为切点),若|PA|=|PB|若O为原点,则|OP|的最小值为( )
| A. | 2 | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\sqrt{5}$ |
1.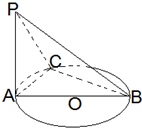 如图,AB是圆O的直径,PA⊥圆O所在的平面,C是圆周上不同于A、B的任意一点,则图中互相垂直的平面共有( )
如图,AB是圆O的直径,PA⊥圆O所在的平面,C是圆周上不同于A、B的任意一点,则图中互相垂直的平面共有( )
 如图,AB是圆O的直径,PA⊥圆O所在的平面,C是圆周上不同于A、B的任意一点,则图中互相垂直的平面共有( )
如图,AB是圆O的直径,PA⊥圆O所在的平面,C是圆周上不同于A、B的任意一点,则图中互相垂直的平面共有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |