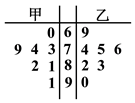题目内容
【题目】若函数f(x)=- ![]() x3+
x3+ ![]() x2+2ax在
x2+2ax在 ![]() 上存在单调递增区间,则a的取值范围是 .
上存在单调递增区间,则a的取值范围是 .
【答案】![]()
【解析】对f(x)求导,得f′(x)=-x2+x+2a
=- ![]() 2+
2+ ![]() +2a.
+2a.
当x∈ ![]() 时,f′(x)的最大值为f′
时,f′(x)的最大值为f′ ![]() =
= ![]() +2a.
+2a.
令 ![]() +2a>0,解得a>-
+2a>0,解得a>- ![]() .
.
所以a的取值范围是 ![]() .
.
求出函数的导数,利用导函数值大于0,转化为a的表达式,求出最值即可得到a的范围.导数和函数的单调性的关系:
(1)若f′(x)>0在(a,b)上恒成立,则f(x)在(a,b)上是增函数,f′(x)>0的解集与定义域的交集的对应区间为增区间;
(2)若f′(x)<0在(a,b)上恒成立,则f(x)在(a,b)上是减函数,f′(x)<0的解集与定义域的交集的对应区间为减区间.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
【题目】某化工厂为预测产品的回收率 ![]() ,需要研究它和原料有效成分含量
,需要研究它和原料有效成分含量 ![]() 之间的相关关系,现收集了4组对照数据。
之间的相关关系,现收集了4组对照数据。
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
(Ⅰ)请根据相关系数 ![]() 的大小判断回收率
的大小判断回收率 ![]() 与
与 ![]() 之间是否存在高度线性相关关系;
之间是否存在高度线性相关关系;
(Ⅱ)请根据上表提供的数据,用最小二乘法求出 ![]() 关于
关于 ![]() 的线性回归方程
的线性回归方程 ![]() ,并预测当
,并预测当 ![]() 时回收率
时回收率 ![]() 的值.
的值.
参考数据: 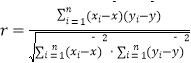
| 1 | 0 |
|
| 其他 |
| 完全相关 | 不相关 | 高度相关 | 低度相关 | 中度相关 |
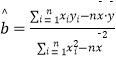 ,
, ![]()