题目内容
直线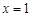 与抛物线
与抛物线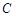 :
: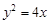 交于
交于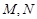 两点,点
两点,点 是抛物线
是抛物线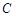 准线上的一点,
准线上的一点,
记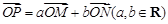 ,其中
,其中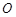 为抛物线
为抛物线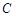 的顶点.
的顶点.
(1)当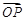 与
与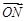 平行时,
平行时,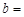 ________;
________;
(2)给出下列命题:
①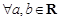 ,
,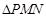 不是等边三角形;
不是等边三角形;
②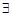
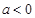 且
且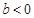 ,使得
,使得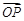 与
与 垂直;
垂直;
③无论点 在准线上如何运动,
在准线上如何运动,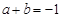 总成立.
总成立.
其中,所有正确命题的序号是___.
【答案】
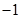 ;①②③
;①②③
【解析】
试题分析:由抛物线方程知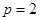 ,焦点
,焦点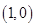 ,准线为
,准线为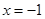 。
。
(1)当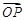 与
与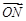 平行时,因为有公共点
平行时,因为有公共点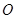 ,所以
,所以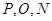 三点共线。因为点
三点共线。因为点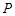 在准线
在准线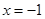 上,点
上,点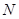 在直线
在直线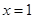 上,所以
上,所以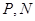 关于点
关于点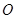 对称,所以
对称,所以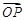 与
与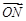 是相反向量,所以
是相反向量,所以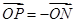 ,此时
,此时 。(2)将
。(2)将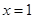 代入
代入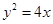 得
得 ,所以
,所以 ,假设
,假设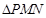 能是等边三角形,则此时点
能是等边三角形,则此时点 只能是准线与
只能是准线与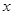 轴交点
轴交点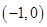 。但此时
。但此时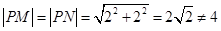 。所以假设不成立,即
。所以假设不成立,即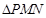 不可能是等边三角形,故①正确;不妨设
不可能是等边三角形,故①正确;不妨设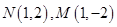 ,设
,设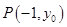 则
则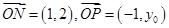 ,
,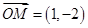 ,当
,当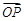 与
与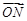 垂直时,
垂直时,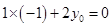 ,解得
,解得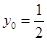 ,即
,即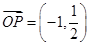 。因为
。因为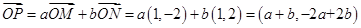 ,所以
,所以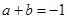 且
且 ,解得
,解得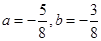 。故②正确;因为
。故②正确;因为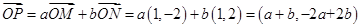 ,且
,且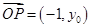 ,所以
,所以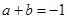 。故③正确。综上可得正确的序号是①②③。
。故③正确。综上可得正确的序号是①②③。
考点:抛物线方程及基本性质,平面向量的平行、垂直及向量坐标的运算法则。

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 ,焦点为F,有一定点
,焦点为F,有一定点 ,A在抛物线准线上的射影为H,P为抛物线上一动点.
,A在抛物线准线上的射影为H,P为抛物线上一动点. ;
; 是过点A且垂直于x轴的直线,是否存在直线
是过点A且垂直于x轴的直线,是否存在直线 ,使得
,使得 的范围;若不存在,请
的范围;若不存在,请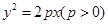 上一动点
上一动点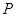 ,抛物线内一点
,抛物线内一点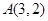 ,
,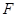 为焦点且
为焦点且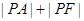 的最小值为
的最小值为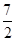 。
。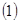 求抛物线方程以及使得|PA|+|PF|最小时的P点坐标;
求抛物线方程以及使得|PA|+|PF|最小时的P点坐标; 过(1)中的P点作两条互相垂直的直线与抛物线分别交于C、D两点,直线CD是否过一定点? 若是,求出该定点坐标; 若不是,请说明理由。
过(1)中的P点作两条互相垂直的直线与抛物线分别交于C、D两点,直线CD是否过一定点? 若是,求出该定点坐标; 若不是,请说明理由。 ,焦点为F,有一定点
,焦点为F,有一定点 ,A在抛物线准线上的射影为H,P为抛物线上一动点.
,A在抛物线准线上的射影为H,P为抛物线上一动点. ;
; 是过点A且垂直于x轴的直线,是否存在直线
是过点A且垂直于x轴的直线,是否存在直线 ,使得
,使得 的范围;若不存在,请
的范围;若不存在,请 上一动点P,抛物线内一点A(3,2) ,F为焦点且
上一动点P,抛物线内一点A(3,2) ,F为焦点且 的最小值为
的最小值为 .
. 取最小值时的P点坐标;
取最小值时的P点坐标;