题目内容
已知P={y|y=x2-2x+3,0≤x≤3},Q={x|y=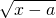 }.
}.
(1)若P∩Q={x|4≤x≤6},求实数a的值
(2)若P∪Q=Q,求实数a的取值范围.
解:(1)∵P={y|y=x2-2x+3,0≤x≤3}={y|y=(x-1)2+2,0≤x≤3}={y|2≤y≤6},
Q={x|y=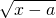 }={x|≥a},P∩Q={x|4≤x≤6},
}={x|≥a},P∩Q={x|4≤x≤6},
∴a=4.
(2)若P∪Q=Q,则P⊆Q,如图:
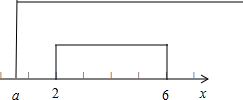
故有 a≤2,故实数a的取值范围为(-∞,].
分析:(1)求出二次函数在闭区间上的最值,可得集合P,再求出集合Q,根据P∩Q={x|4≤x≤6},求出a的值.
(2)若P∪Q=Q,则P⊆Q,结合图形可得a≤2,从而求得实数a的取值范围.
点评:本题主要考查二次函数在闭区间上的最值,集合关系中参数的取值范围问题,体现了数形结合的数学思想,属于中档题.
Q={x|y=
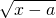 }={x|≥a},P∩Q={x|4≤x≤6},
}={x|≥a},P∩Q={x|4≤x≤6},∴a=4.
(2)若P∪Q=Q,则P⊆Q,如图:

故有 a≤2,故实数a的取值范围为(-∞,].
分析:(1)求出二次函数在闭区间上的最值,可得集合P,再求出集合Q,根据P∩Q={x|4≤x≤6},求出a的值.
(2)若P∪Q=Q,则P⊆Q,结合图形可得a≤2,从而求得实数a的取值范围.
点评:本题主要考查二次函数在闭区间上的最值,集合关系中参数的取值范围问题,体现了数形结合的数学思想,属于中档题.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
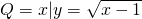 ,则P∩Q=________.
,则P∩Q=________.