题目内容
(2012•山东)在等差数列{an}中,a3+a4+a5=84,a9=73.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)对任意m∈N*,将数列{an}中落入区间(9m,92m)内的项的个数记为bm,求数列{bm}的前m项和Sm.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)对任意m∈N*,将数列{an}中落入区间(9m,92m)内的项的个数记为bm,求数列{bm}的前m项和Sm.
分析:(I)由已知及等差数列的性质可求a4,由d=
可求公差d,进而可求a1,进而可求通项
(II)由9m<an<92m可得9m+8<9n<92m+8,从而可得bm=92m-1-9m-1,由等比数列的求和公式可求
| a9-a4 |
| 9-4 |
(II)由9m<an<92m可得9m+8<9n<92m+8,从而可得bm=92m-1-9m-1,由等比数列的求和公式可求
解答:解:(I)∵数列{an}是等差数列
∴a3+a4+a5=3a4=84,
∴a4=28
设等差数列的公差为d
∵a9=73
∴d=
=
=9
由a4=a1+3d可得28=a1+27
∴a1=1
∴an=a1+(n-1)d=1+9(n-1)=9n-8
(II)若9m<an<92m
则9m+8<9n<92m+8
因此9m-1+1≤n≤92m-1
故得bm=92m-1-9m-1
∴Sm=b1+b2+…+bm
=(9+93+95+…+92m-1)-(1+9+…+9m-1)
=
-
=
∴a3+a4+a5=3a4=84,
∴a4=28
设等差数列的公差为d
∵a9=73
∴d=
| a9-a4 |
| 9-4 |
| 73-28 |
| 5 |
由a4=a1+3d可得28=a1+27
∴a1=1
∴an=a1+(n-1)d=1+9(n-1)=9n-8
(II)若9m<an<92m
则9m+8<9n<92m+8
因此9m-1+1≤n≤92m-1
故得bm=92m-1-9m-1
∴Sm=b1+b2+…+bm
=(9+93+95+…+92m-1)-(1+9+…+9m-1)
=
| 9(1-81m) |
| 1-81 |
| 1-9m |
| 1-9 |
=
| 92m+1-10×9m+1 |
| 80 |
点评:本题主要考查了等差数列的性质及通项公式的应用,等比数列的求和公式的应用,属于等差数列与等比数列基本运算的综合应用.

练习册系列答案
相关题目
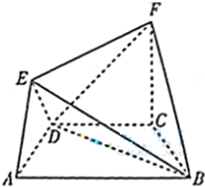 (2012•山东)在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF.
(2012•山东)在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF.