��Ŀ����
��2012•ɽ������ƽ��ֱ������ϵxOy�У�F��������C��x2=2py��p��0���Ľ��㣬M��������C��λ�ڵ�һ�����ڵ�����һ�㣬��M��F��O�����Բ��Բ��ΪQ����Q��������C���ߵľ���Ϊ
��
������������C�ķ��̣�
�����Ƿ���ڵ�M��ʹ��ֱ��MQ��������C�����ڵ�M�������ڣ������M�����ꣻ�������ڣ�˵�����ɣ�
��������M�ĺ�����Ϊ
��ֱ��l��y=kx+
��������C��������ͬ�Ľ���A��B��l��ԲQ��������ͬ�Ľ���D��E����
��k��2ʱ��|AB|2+|DE|2����Сֵ��
| 3 |
| 4 |
������������C�ķ��̣�
�����Ƿ���ڵ�M��ʹ��ֱ��MQ��������C�����ڵ�M�������ڣ������M�����ꣻ�������ڣ�˵�����ɣ�
��������M�ĺ�����Ϊ
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
����������ͨ��F��0��
����Բ��Q���߶�OFƽ����y=
�ϣ��Ƴ����p=1���Ƴ�������C�ķ��̣�
��������ڵ�M��x0��
������x0��0������������������C�ڵ�M�������ߵ�б��Ϊ�����ĵ��������Q�����꣬����|QM|=|OQ|�����M��
��1����ʹ��ֱ��MQ��������C�������M��
����x0=
ʱ�������Q�ķ���Ϊ������ֱ���������߷������������飮��A��x1��y1����B��x2��y2��������Τ�ﶨ�������|AB|2��ͬ�����|DE|2��ͨ��|AB|2+|DE|2�ı���ʽ��ͨ����Ԫ�����õ��������������Сֵ��
| P |
| 2 |
| p |
| 4 |
��������ڵ�M��x0��
| x02 |
| 2 |
| 2 |
����x0=
| 2 |
����⣺�����������֪F��0��
����Բ��Q���߶�OFƽ����y=
�ϣ�
��Ϊ������C�ı�����Ϊy=-
��
����
=
����p=1��
���������C�ķ���x2=2y��
��������ڵ�M��x0��
������x0��0������������
������C�ڵ�M�������ߵ�б��Ϊ
y��
=(
) ��
=x0��
��y=
�ã�xQ=
+
��
����Q��
+
��
����
��|QM|=|OQ|��
��( -
+
)2+(
-
) 2=(
+
)2+
��
���(
-
) 2=
����x0��0��
����x0=
����ʱM��
��1����
�ʴ��ڵ�M��
��1����ʹ��ֱ��MQ��������C�������M��
����x0=
ʱ���ɣ���Q��
��
������Q�İ뾶Ϊ��r=
=
��
���ԡ�Q�ķ���Ϊ(x-
)2+(y-
)2=
��
��
��������2x2-4kx-1=0��
��A��x1��y1����B��x2��y2�������ڡ�=16k2+8��0��x1+x2=2k��x1x2=-
��
����|AB|2=��1+k2��[��x1+x2��2-4x1x2]=��1+k2����4k2+2����
��
�������ã�1+k2��x2-
x-
=0��
��D��E���������ֱ�Ϊ��x3��y3������x4��y4����
���ڡ�=
+
��0��x3+x4=
��x3x4=-
��
����|DE|2=��1+k2��[��x3+x4��2-4x3x4]=
+
��
���|AB|2+|DE|2=��1+k2����4k2+2��+
+
����1+k2=t������
��t��5����
��t��5��
����|AB|2+|DE|2=t��4t-2��+
+
=4t2-2t+
+
��
��g��t��=4t2-2t+
+
��t�� [
��5]����Ϊg�䣨t��=8t-2-
��
���Ե�t�� [
��5]��g�䣨t����g�䣨
��=6��
������g��t����t�� [
��5]�������������Ե�t=
ʱ��g��t��ȡ��Сֵ
��
��˵�k=
ʱ��|AB|2+|DE|2����СֵΪ
��
| P |
| 2 |
| p |
| 4 |
��Ϊ������C�ı�����Ϊy=-
| p |
| 2 |
����
| 3p |
| 4 |
| 3 |
| 4 |
���������C�ķ���x2=2y��
��������ڵ�M��x0��
| x02 |
| 2 |
������C�ڵ�M�������ߵ�б��Ϊ
y��
| | | x=x0 |
| x2 |
| 2 |
| | | x=x0 |
��y=
| 1 |
| 4 |
| x0 |
| 2 |
| 1 |
| 4x0 |
����Q��
| x0 |
| 2 |
| 1 |
| 4x0 |
| 1 |
| 4 |
��|QM|=|OQ|��
��( -
| x0 |
| 2 |
| 1 |
| 4x0 |
| 1 |
| 4 |
| x02 |
| 2 |
| x0 |
| 2 |
| 1 |
| 4x0 |
| 1 |
| 16 |
���(
| 1 |
| 4 |
| x02 |
| 2 |
| 9 |
| 16 |
����x0=
| 2 |
| 2 |
�ʴ��ڵ�M��
| 2 |
����x0=
| 2 |
5
| ||
| 8 |
| 1 |
| 4 |
(
|
3
| ||
| 8 |
���ԡ�Q�ķ���Ϊ(x-
5
| ||
| 8 |
| 1 |
| 4 |
| 27 |
| 32 |
��
|
��A��x1��y1����B��x2��y2�������ڡ�=16k2+8��0��x1+x2=2k��x1x2=-
| 1 |
| 2 |
����|AB|2=��1+k2��[��x1+x2��2-4x1x2]=��1+k2����4k2+2����
��
|
5
| ||
| 4 |
| 1 |
| 16 |
��D��E���������ֱ�Ϊ��x3��y3������x4��y4����
���ڡ�=
| k2 |
| 4 |
| 27 |
| 8 |
5
| ||
| 4(1+ k 2) |
| 1 |
| 16(1+ k 2) |
����|DE|2=��1+k2��[��x3+x4��2-4x3x4]=
| 25 |
| 8(1+ k 2) |
| 1 |
| 4 |
���|AB|2+|DE|2=��1+k2����4k2+2��+
| 25 |
| 8(1+ k 2) |
| 1 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
����|AB|2+|DE|2=t��4t-2��+
| 25 |
| 8t |
| 1 |
| 4 |
| 25 |
| 8t |
| 1 |
| 4 |
��g��t��=4t2-2t+
| 25 |
| 8t |
| 1 |
| 4 |
| 5 |
| 4 |
| 25 |
| 8t2 |
���Ե�t�� [
| 5 |
| 4 |
| 5 |
| 4 |
������g��t����t�� [
| 5 |
| 4 |
| 5 |
| 4 |
| 13 |
| 2 |
��˵�k=
| 1 |
| 2 |
| 13 |
| 2 |
���������⿼��ֱ����Բ���ߵ��ۺ����⣬�����ߵı����̣������ߵļ����ʣ��������Ľ��ⷽ�����ҳ���ʽ��Ӧ�ã�������������������������ת��˼���Ӧ�ã�

��ϰ��ϵ�д�
�����Ŀ
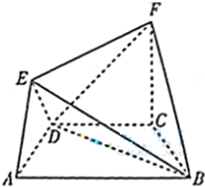 ��2012•ɽ��������ͼ��ʾ�ļ������У��ı���ABCD�ǵ������Σ�AB��CD����DAB=60�㣬FC��ƽ��ABCD��AE��BD��CB=CD=CF��
��2012•ɽ��������ͼ��ʾ�ļ������У��ı���ABCD�ǵ������Σ�AB��CD����DAB=60�㣬FC��ƽ��ABCD��AE��BD��CB=CD=CF��