��Ŀ����
��֪���κ���f��t��=at2-| b |
| 1 |
| 4a |
| x-a |
| x |
��1����A��B��
��2�����壺��A-B={x��A����x∉B}����a��b��x��Ϊ��������x��A����P��E��Ϊxȡ�Լ���A-B�ĸ��ʣ�P��F��xȡ����A��B�ĸ��ʣ���֪P��E��=
| 2 |
| 3 |
| 1 |
| 3 |
����a1��a2��a3��b1��b2��b3��
����д������{an}��{bn}��ͨ�ʽ������֤������
������ں�����f��t���У�a=an��b=bn����f��t�������ֵΪg��n����cn=
| 1-12g(n) |
| 4g(n) |
��������1����f��t�������ֵ��֪a��0����f��t��max=
��b��1���ɴ����������A��B��
��2������ΪP��E��=
��P��F��=
������A�������ĸ������ֱ����a1��a2��a3��b1��b2��b3��
��an=-3n-1��bn=n+1��
����g��n��=
=
��֪cn=
=
���ɴ��ܹ�֤��Sn��1��
| 1-b |
| 4a |
��2������ΪP��E��=
| 2 |
| 3 |
| 1 |
| 3 |
��an=-3n-1��bn=n+1��
����g��n��=
| 1-bn |
| 4an |
| n |
| 4(3n+1) |
| 1-12g(n) |
| 4g(n) |
| 1 |
| n |
����⣺��1����f��t�������ֵ����a��0��
��f��t��max=
��b��1����2�֣�
��A={x|a��x��0}��B={x|-b��x��b}��4�֣�
��2������ΪP��E��=
��P��F��=
���Կ���һ�����Σ�
��A����3������ʱ��A-B����2����A��B����1������a=-4��b=2��
��A����6������ʱ��A-B����4����A��B����2������a=-7��b=3��
��A����9������ʱ��A-B����6����A��B����3������a=-10��b=4��
��a1=-4��a2=-7��a3=-10��b1=2��b2=3��b3=4��7�֣�
��an=-3n-1��bn=n+1��19�֣�
�ۡ�g��n��=
=
����cn=
=
��
��cncn+1=
��
=
-
����Sn=��1-
��+��
-
��++��
-
��=1-
��1
��13�֣�
��f��t��max=
| 1-b |
| 4a |
��A={x|a��x��0}��B={x|-b��x��b}��4�֣�
��2������ΪP��E��=
| 2 |
| 3 |
| 1 |
| 3 |
��A����3������ʱ��A-B����2����A��B����1������a=-4��b=2��
��A����6������ʱ��A-B����4����A��B����2������a=-7��b=3��
��A����9������ʱ��A-B����6����A��B����3������a=-10��b=4��
��a1=-4��a2=-7��a3=-10��b1=2��b2=3��b3=4��7�֣�
��an=-3n-1��bn=n+1��19�֣�
�ۡ�g��n��=
| 1-bn |
| 4an |
| n |
| 4(3n+1) |
| 1-12g(n) |
| 4g(n) |
| 1 |
| n |
��cncn+1=
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
��13�֣�
���������⿼�����е����ʺ�Ӧ�ã�����ʱҪ�������⣬��ϸ��⣬ע�ʽ�ĺ������ã�

��ϰ��ϵ�д�
�����Ŀ
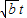 +
+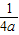 ��t��R�������ֵ�����ֵΪ��ʵ��������A=
��t��R�������ֵ�����ֵΪ��ʵ��������A=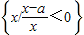 ������B=
������B=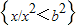 ��
��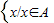 ��x∉B����x��A��P��E��Ϊxȡ��A-B�ĸ��ʣ�P��F��Ϊxȡ��A/B�ĸ��ʣ�����������⣺
��x∉B����x��A��P��E��Ϊxȡ��A-B�ĸ��ʣ�P��F��Ϊxȡ��A/B�ĸ��ʣ�����������⣺ ��P��F��=
��P��F��= ��
��