Question

定义域为R的函数f（x）满足以下两个条件：
①对于任意的x，y?R，均有f（x+y）=f（x）f（1-y）+f（1-x）f（y）成立；
②（x）在[0，1]上单调递增．
（Ⅰ） 求证：f（1）=1；
（Ⅱ） 判断f（x）的奇偶性，并说明理由；
（Ⅲ） 求满足f(2x-1)≥

1

2

的实数x的集合．

Answer 1

分析：（Ⅰ） 通过赋值法，x=y=0，令x=0，y=1，以及x=y=

1

2

，推出f（0）＜f（1），求出f（1）=1；
（Ⅱ） 说明函数f（x）的奇偶性，通过令y=-x，得f（0）=f（x）f（x+1）+f（1-x）f（-x）．令y=1，得f（x+1）=f（x）f（0）+f（1-x）f（1）=f（1-x）．推出对于任意的x∈R，恒有f（-x）=-f（x），f（x）为奇函数．
（Ⅲ） 推出函数的周期，根据函数在[-2，2]的图象以及函数的周期性，即可求满足f(2x-1)≥

1

2

的实数x的集合．

解答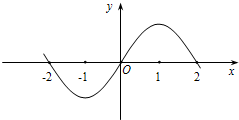：解：（Ⅰ）证明：令x=y=0，得 f（0）=2f（0）f（1），所以f（0）=0或f(1)=

1

2

．（1分）
令x=0，y=1，得f（1）=[f（0）]²+[f（1）]²．
若f(1)=

1

2

，则f(0)=±

1

2

．
令x=y=

1

2

，得f(1)=2[f(

1

2

)]2．
即f(

1

2

)=±

1

2

，
因为f（x）在[0，1]上单调递增，所以f（0）＜f(

1

2

)＜f(1)，矛盾！
因此f（0）=0，f（1）=[f（1）]²，f（1）=1．（3分）
（Ⅱ） f（x）是奇函数                   （4分）
令y=-x，得f（0）=f（x）f（x+1）+f（1-x）f（-x）．…①
令y=1，得f（x+1）=f（x）f（0）+f（1-x）f（1）=f（1-x）．…②
即对于任意的x∈R，恒有f（x-1）=-f（1-x），
代入①式得对于任意的x∈R，恒有f（-x）=-f（x），所以f（x）为奇函数．（6分）
（Ⅲ）由（Ⅱ）可得f（x）=f（2-x）=-f（x-2）=-f（4-x）=f（x-4），
即：函数f（x）的最小正周期为4．
令x=y=

1

3

，f(

2

3

)=2f(

1

3

)f(

2

3

)，因为f(

2

3

)＞f(0)=0，，所以f(

1

3

)=

1

2

．
由②得：f(

5

3

)=

1

2

．
根据函数在[-2，2]的图象以及函数的周期性，
观察得，若f(2x-1)≥

1

2

，
则

1

3

+4k≤2x-1≤

5

3

+4k，k∈Z，
所以

2

3

+2k≤x≤

4

3

+2k，k∈Z，x∈{x|

2

3

+2k≤x≤

4

3

+2k，k∈Z}（8分）

点评：本题是综合题，考查赋值法求函数值的应用，函数奇偶性的判断与证明，函数图象的应用，不等式的解法．运算能力，理解能力要求比较高．