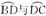Question

如图所示，球O的半径为2，AC是球的直径，AB⊥BC，球O的截面BDC把球面面积分成3∶1的两部分，BC是截面圆的直径，D是底面圆周上的一点，且满足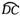、的弧长之比为1∶2.

（1）证明平面ABD⊥平面ADC；

（2）求异面直线AC和BD所成的角.

Answer 1

（1）证明:设截面圆圆心为O₁，则OO₁⊥BC于O₁，AB⊥BC，且A、B、C、O、O₁共面，

∴AB∥OO₁.∵OO₁⊥平面BCD，

∴AB⊥平面BCD.∴AB⊥DC.又BD⊥DC,

∴DC⊥平面ABD.

∵DC平面ADC，

∴平面ABD⊥平面ADC.

（2）解:在截面圆O₁中，作CEBD，由平面几何知识，E在圆O₁的圆周上，连结EA、BE，同（1）可证CE⊥AE，

易知AB=2OO₁=2，BC=.

∵与的弧长之比为1∶2，

∴BD=CE=,DC=BE=3.在Rt△ABE中，AE=，

在Rt△AEC 中，tan∠ACE=,

∴所求角为arctan.