题目内容
已知圆A的圆心为(| 2 |
(1)求双曲线C的方程;
(2)设直线l过点A,斜率为k,当0<k<1时,双曲线C的上支上有且仅有一点B到直线l的距离为
| 2 |
分析:(1)设双曲线的渐近线为y=kx,则可求得圆心到直线的距离求得k,进而求得点A的关于直线y=x的对称点,求得双曲线的a和b,双曲线方程可得.
(2)依题意设B点在与l平行的直线l'上,且l与l'间的距离为
,设直线l':y=kx+m,则可表示出B点到直线l的距离求得m与k的关系式,把l'代入双曲线方程,根据判别式等于0求得m和k的另一个关系式,联立求得m和k,进而求得B点的坐标.
(2)依题意设B点在与l平行的直线l'上,且l与l'间的距离为
| 2 |
解答:解:(1)设双曲线的渐近线为y=kx,则
=1,解得k=±1.即渐近线为y=±x.
又点A关于y=x的对称点A'的坐标为(0,
),
所以,a=b=
,双曲线的方程为
-
=1.
(2)直线l:y=k(x-
),(0<k<1).
依题意设B点在与l平行的直线l'上,且l与l'间的距离为
,设直线l':y=kx+m,则
=
,即m2+2
km=2①
把l'代入双曲线方程得:(k2-1)x2+2mkx+m2-2=0
∵0<k<1,∴k2-1≠0.∴△=4(m2+2k2-2)=0,即m2+2k2=2②
解①②,得m=
,k=
.
此时,x=2
,y=
,所以B(2
,
).
|
| ||
|
又点A关于y=x的对称点A'的坐标为(0,
| 2 |
所以,a=b=
| 2 |
| y2 |
| 2 |
| x2 |
| 2 |
(2)直线l:y=k(x-
| 2 |
依题意设B点在与l平行的直线l'上,且l与l'间的距离为
| 2 |
|
| ||
|
| 2 |
| 2 |
把l'代入双曲线方程得:(k2-1)x2+2mkx+m2-2=0
∵0<k<1,∴k2-1≠0.∴△=4(m2+2k2-2)=0,即m2+2k2=2②
解①②,得m=
| ||
| 5 |
2
| ||
| 5 |
此时,x=2
| 2 |
| 10 |
| 2 |
| 10 |
点评:本题主要考查了双曲线的标准方程.圆锥曲线与直线的关系历来是高考的热点,应加强复习.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
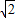 ,0),半径为1,双曲线C的两条渐近线都过原点,且与圆A相切,双曲线C的一个顶点A′与点A关于直线y=x对称.
,0),半径为1,双曲线C的两条渐近线都过原点,且与圆A相切,双曲线C的一个顶点A′与点A关于直线y=x对称.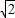 ,试求k的值及此时点B的坐标.
,试求k的值及此时点B的坐标.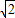 ,0),半径为1,双曲线C的两条渐近线都过原点,且与圆A相切,双曲线C的一个顶点A′与点A关于直线y=x对称.
,0),半径为1,双曲线C的两条渐近线都过原点,且与圆A相切,双曲线C的一个顶点A′与点A关于直线y=x对称.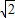 ,试求k的值及此时点B的坐标.
,试求k的值及此时点B的坐标.