题目内容
已知全集 ,集合
,集合 ,则
,则 .
.

解析试题分析:根据题意,由于全集 ,集合
,集合 ,那么
,那么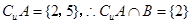 ,故可知结论为
,故可知结论为
考点:交集与并集
点评:解决的关键是根据集合的交集和并集来求解运算,属于基础题,送分试题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
已知全集 ,集合
,集合 ,则
,则 .
.

解析试题分析:根据题意,由于全集 ,集合
,集合 ,那么
,那么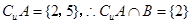 ,故可知结论为
,故可知结论为
考点:交集与并集
点评:解决的关键是根据集合的交集和并集来求解运算,属于基础题,送分试题。

 名校课堂系列答案
名校课堂系列答案