题目内容
已知函数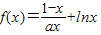 ,
,(1)若函数f(x)在[1,+∞)上为递增函数,求正实数a的取值范围;
(2)当a=1时,求函数f(x)在
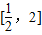 上的最大值和最小值;
上的最大值和最小值;(3)试比较
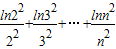 与
与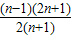 的大小,并说明理由.
的大小,并说明理由.
【答案】分析:(1)求导函数,确定函数的单调区间,利用函数f(x)在[1,+∞)上为递增函数,可得[1,+∞)是单调增区间的子集,由此可确定正实数a的取值范围;
(2)确定函数在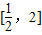 上的单调性,进而可求函数f(x)在
上的单调性,进而可求函数f(x)在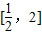 上的最大值和最小值;
上的最大值和最小值;
(3)令a=1,由(1)得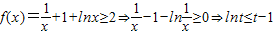 (当且仅当t=1时等号成立),
(当且仅当t=1时等号成立),
两边同除t(t>0)得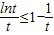 ,再令t=n2,进而利用累加法,即可得到结论.
,再令t=n2,进而利用累加法,即可得到结论.
解答:解:(1)由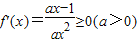 ,可得
,可得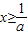 ,∴函数f(x)在
,∴函数f(x)在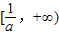 递增,
递增,
∵函数f(x)在[1,+∞)上为递增函数
∴[1,+∞)是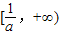 的子集,
的子集,
∴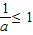
∵a>0,∴a≥1.
(2)当a=1,由(1)的函数f(x)在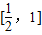 上递减,在[1,2]上递增.
上递减,在[1,2]上递增.
则ymin=f(1)=2;
又因为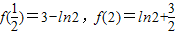 ,
,
∴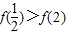
∴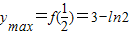 .
.
(3)令a=1,
由(1)得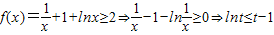 (当且仅当t=1时等号成立),
(当且仅当t=1时等号成立),
两边同除t(t>0)得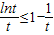 ,
,
令t=n2,
可得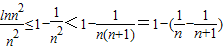
由累加法得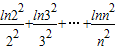
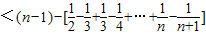 =
=
点评:本题重点考查导数知识的运用,考查函数的单调性,考查函数的最值,考查大小比较,解题的关键是正确求出导函数,合理构建不等式,属于中档题.
(2)确定函数在
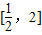 上的单调性,进而可求函数f(x)在
上的单调性,进而可求函数f(x)在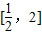 上的最大值和最小值;
上的最大值和最小值;(3)令a=1,由(1)得
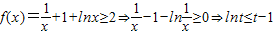 (当且仅当t=1时等号成立),
(当且仅当t=1时等号成立),两边同除t(t>0)得
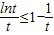 ,再令t=n2,进而利用累加法,即可得到结论.
,再令t=n2,进而利用累加法,即可得到结论.解答:解:(1)由
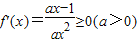 ,可得
,可得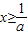 ,∴函数f(x)在
,∴函数f(x)在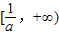 递增,
递增,∵函数f(x)在[1,+∞)上为递增函数
∴[1,+∞)是
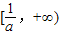 的子集,
的子集,∴
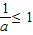
∵a>0,∴a≥1.
(2)当a=1,由(1)的函数f(x)在
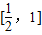 上递减,在[1,2]上递增.
上递减,在[1,2]上递增.则ymin=f(1)=2;
又因为
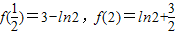 ,
,∴
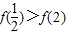
∴
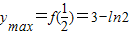 .
.(3)令a=1,
由(1)得
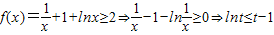 (当且仅当t=1时等号成立),
(当且仅当t=1时等号成立),两边同除t(t>0)得
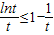 ,
,令t=n2,
可得
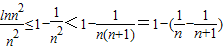
由累加法得
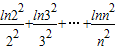
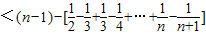 =
=
点评:本题重点考查导数知识的运用,考查函数的单调性,考查函数的最值,考查大小比较,解题的关键是正确求出导函数,合理构建不等式,属于中档题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目





 的定义域为
的定义域为 ,部分函数值如表所示,其导函数的图象如图所示,若正数
,部分函数值如表所示,其导函数的图象如图所示,若正数 ,
, 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( ) 



 B.
B. C.
C. D.
D.
 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。