Question

下列命题中是真命题的是

①②

（写出所有你认为是真命题的序号）
①命题p：?x∈R，x²+1≥1；命题q：?x∈R，x²-x+1≤0，则p∧（￢q）是真命题；
②若不等式(m+n)(

a

m

+

1

n

)≥25(a＞0)对?m，n∈R⁺恒成立，则a的最小值为16；
③函数f（x）=sinx-x的零点有3个；
④若函数f（x）=sin（2x+φ）的图象关于y轴对称，则φ=

π

2

；
⑤“a，b，c成等比数列”是“b=

ac

”的充要条件．

Answer 1

分析：①由命题p是真命题，命题q是假命题，知p∧（￢q）是真命题；
②由（m+n）（

a

m

+

1

n

）=a+1+

na

m

+

m

n

≥a+1+2

a

≥25，能求出a的最小值；
③在同一坐标系内画出函数y=sinx与y=x的图象，利用图象得结论．；
④若函数f（x）=sin（2x+φ）的图象关于y轴对称，则φ=

π

2

+kπ；
⑤“a，b，c成等比数列”是“b=

ac

”的充分不必要条件．

解答：解：①∵命题p：?x∈R，x²+1≥1是真命题，
命题q：?x∈R，x²-x+1=（x-

1

2

）²+

3

4

≤0是假命题，
∴p∧（￢q）是真命题，故①正确；
②∵不等式(m+n)(

a

m

+

1

n

)≥25(a＞0)对?m，n∈R⁺恒成立，
∴（m+n）（

a

m

+

1

n

）=a+1+

na

m

+

m

n

≥a+1+2

a

≥25，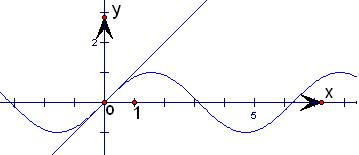
∴a的最小值为16，故②正确；
③∵因为函数的零点个数就是找对应两个函数的图象的交点个数，
在同一坐标系内画出函数y=sinx与y=x的图象，
由图得交点1个，
故函数f（x）=sinx-x的零点的个数是1．故③错误；
④若函数f（x）=sin（2x+φ）的图象关于y轴对称，则φ=

π

2

+kπ，故④不正确；
⑤“a，b，c成等比数列”是“b=

ac

”的充分不必要条件，故⑤不正确．
故答案为：①②．

点评：本题考查命题的真假判断，解题时要认真审题，注意不等式、均值定理、函数零点、三角函数、数列等基本知识点的合理运用．