题目内容
【题目】如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2. 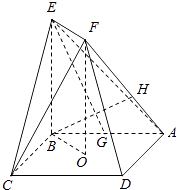
(1)求证:EG∥平面ADF;
(2)求二面角O﹣EF﹣C的正弦值;
(3)设H为线段AF上的点,且AH= ![]() HF,求直线BH和平面CEF所成角的正弦值.
HF,求直线BH和平面CEF所成角的正弦值.
【答案】
(1)证明:取AD的中点I,连接FI,
∵矩形OBEF,∴EF∥OB,EF=OB,
∵G,I是中点,
∴GI∥BD,GI= ![]() BD.
BD.
∵O是正方形ABCD的中心,
∴OB= ![]() BD.
BD.
∴EF∥GI,EF=GI,
∴四边形EFIG是平行四边形,
∴EG∥FI,
∵EG平面ADF,FI平面ADF,
∴EG∥平面ADF
(2)解:建立如图所示的坐标系O﹣xyz,则B(0,﹣ ![]() ,0),C(
,0),C( ![]() ,0,0),E(0,﹣
,0,0),E(0,﹣ ![]() ,2),
,2),
F(0,0,2),
设平面CEF的法向量为 ![]() =(x,y,z),则
=(x,y,z),则  ,取
,取 ![]() =(
=( ![]() ,0,1)
,0,1)
∵OC⊥平面OEF,
∴平面OEF的法向量为 ![]() =(1,0,0),
=(1,0,0),
∵|cos< ![]() ,
, ![]() >|=
>|= ![]()
∴二面角O﹣EF﹣C的正弦值为  =
= ![]()
(3)解:AH= ![]() HF,∴
HF,∴ ![]() =
= ![]()
![]() =(
=( ![]() ,0,
,0, ![]() ).
).
设H(a,b,c),则 ![]() =(a+
=(a+ ![]() ,b,c)=(
,b,c)=( ![]() ,0,
,0, ![]() ).
).
∴a=﹣ ![]() ,b=0,c=
,b=0,c= ![]() ,
,
∴ ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,
, ![]() ),
),
∴直线BH和平面CEF所成角的正弦值=|cos< ![]() ,
, ![]() >|=
>|=  =
= ![]() .
.

【解析】(1)取AD的中点I,连接FI,证明四边形EFIG是平行四边形,可得EG∥FI,利用线面平行的判定定理证明:EG∥平面ADF;(2)建立如图所示的坐标系O﹣xyz,求出平面OEF的法向量,平面OEF的法向量,利用向量的夹角公式,即可求二面角O﹣EF﹣C的正弦值;(3)求出 ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,
, ![]() ),利用向量的夹角公式求出直线BH和平面CEF所成角的正弦值.
),利用向量的夹角公式求出直线BH和平面CEF所成角的正弦值.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案【题目】省环保厅对![]() 、
、![]() 、
、![]() 三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
|
|
| |
优(个) | 28 |
|
|
良(个) | 32 | 30 |
|
已知在这180个数据中随机抽取一个,恰好抽到记录![]() 城市空气质量为优的数据的概率为0.2.
城市空气质量为优的数据的概率为0.2.
(1)现按城市用分层抽样的方法,从上述180个数据中抽取30个进行后续分析,求在![]() 城中应抽取的数据的个数;
城中应抽取的数据的个数;
(2)已知![]() ,
, ![]() ,求在
,求在![]() 城中空气质量为优的天数大于空气质量为良的天数的概率.
城中空气质量为优的天数大于空气质量为良的天数的概率.