题目内容
长方体一个顶点上三条棱的长分别为a、b、c,(a、b、c两两不等),一条对角线为AB,长方体的表面上A、B两点间的最短路程为| a2+(b+c)2 |
分析:画出长方体的图形,求出AB的长,结合题意,推导关系.
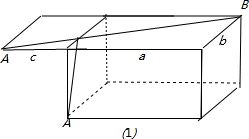
解答:解:在长方体表面上从A到B的最短路途,由于长方体的对称性,可从以下三种实现方式中比较获得:
(1)AB'1=
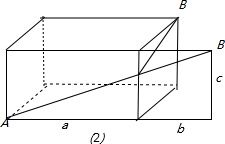
(2)AB'2=
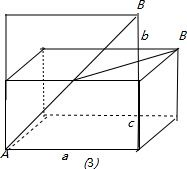
(3)AB'3=
由已知是短路程为第(3)种情况下获得:
∴AB'1>AB'2且AB'3>AB'2,
而AB'1与AB'3则大小关系不定,
∴可知a,b,c的关系为:2ac>2bc且2ab>2bc,2bc与2ab不定.
即a>b且a>c,b,c关系不定.
故选A>b且a>c,b,c关系不定.
(1)AB'1=
| b2+(a+c)2 |
| c2+(a+b)2 |
| a2+(b+c)2 |
由已知是短路程为第(3)种情况下获得:
∴AB'1>AB'2且AB'3>AB'2,
而AB'1与AB'3则大小关系不定,
∴可知a,b,c的关系为:2ac>2bc且2ab>2bc,2bc与2ab不定.
即a>b且a>c,b,c关系不定.



故选A>b且a>c,b,c关系不定.
点评:本题考查棱柱的结构特征,比较大小,考查空间想象能力,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 π B.25
π B.25 π B.25
π B.25