题目内容
如图，圆内切于正方形，向该正方形内随机投掷N个点（假设N足够大，如N＞1000），设落在阴影部分的点N1个，那么由随机模拟思想可得圆周率π的近似值为分析：设出正方形的边长，从而得到圆的半径，写出正方形和圆的面积，根据点落在圆内的概率等于圆的面积除以正方形的面积，列出一个关于π的关系式，做出π的估计值．
解答：解：假设正方形的边长是2，则正方形的面积是4，
圆的半径是1，则圆的面积是π，
根据几何概型的概率公式当得到
=
，
∴π=
．
故答案为：
．
圆的半径是1，则圆的面积是π，
根据几何概型的概率公式当得到
| N1 |
| N |
| π |
| 4 |
∴π=
| 4N1 |
| N |
故答案为：
| 4N1 |
| N |
点评：本题考查模拟方法估计概率，考查几何概型，考查利用实际操作验证数学中常用的π的值，是一个比较好的题目．
练习册系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
（2011•嘉定区一模）如图，在平面直角坐标系xOy中，圆x2+y2=r2（r＞0）内切于正方形ABCD，任取圆上一点P，若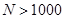
），设落在阴影部分的点N1个，
的近似值为
。
如图，圆内切于正方形，向该正方形内随机投掷N个点（假设N足够大，如N＞1000），设落在阴影部分的点N1个，那么由随机模拟思想可得圆周率π的近似值为________．
=a•
+b•
（a、b∈R），则a、b满足的一个等式是 ．