题目内容
19.已知二次函数f(x)=ax2+bx (a,b为常数,且a≠0),满足条件f(1+x)=f(1-x),且方程f(x)=x有等根.(1)求f(x)的解析式;
(2)设k>0,函数g(x)=kx+1,x∈[-2,1],若对于任意x1∈[-2,1],总存在x0∈[-2,1],使得g(x0)=f(x1)成立,求k的取值范围.
(3)是否存在实数m、n(m<n),使f(x)的定义域和值域分别为[m,n]和[3m,3n],如果存在,求出m、n的值,如果不存在,说明理由.
分析 (1)由已知中f (1+x)=f (1-x),可得f(x)的图象关于直线x=1对称,结合方程f (x)=x有等根其△=0,我们可构造关于a,b的方程组,解方程组求出a,b的值,即可得到f (x)的解析式;
(2)对于任意x1∈[-2,1],总存在x0∈[-2,1],使得g(x0)=f(x1)成立,得到函数f(x)在[-2,1]上值域是g(x)在[-2,1]上值域A的子集,然后利用求函数值域之间的关系列出不等式,解此不等式组即可求得实数a的取值范围即可.
(3)由(1)中函数的解析式,我们根据f(x)的定义域和值域分别为[m,n]和[3m,3n],我们易判断出函数在[m,n]的单调性,进而构造出满足条件的方程,解方程即可得到答案.
解答 解:(1)∵f(x)满足f(1+x)=f(1-x),∴f(x)的图象关于直线x=1对称.
而二次函数f(x)的对称轴为x=-$\frac{b}{2a}$,∴-$\frac{b}{2a}$=1.①
又f(x)=x有等根,即ax2+(b-1)x=0有等根,∴△=(b-1)2=0.②
由①,②得 b=1,a=-$\frac{1}{2}$.∴f(x)=-$\frac{1}{2}$x2+x.
(2)∵f(x)=-$\frac{1}{2}$x2+x,x∈[-2,1],∴函数f(x)的值域为[-4,$\frac{1}{2}$],
若对于任意x1∈[-2,1],总存在x0∈[-2,1],使得g(x0)=f(x1)成立,
则函数f(x)在[-2,1]上值域是g(x)在[-2,1]上值域A的子集,
①若k=0,g(x)=1,不满足条件.
②当k>0时,g(x)=kx+1在[-2,1]是增函数,g(x)∈[-2k+1,k+1],
则[-4,$\frac{1}{2}$]⊆[-2k+1,k+1],
∴$\left\{\begin{array}{l}{-2k+1≤-4}\\{k+1≥\frac{1}{2}}\end{array}\right.$,
∴k≥$\frac{5}{2}$;
③k<0,g(x)=kx+1在[-2,1]是减函数,g(x)∈[k+1,-2k+1],
∴$\left\{\begin{array}{l}{k+1≤-4}\\{-2k+1≥\frac{1}{2}}\end{array}\right.$,
∴k≤-5
综上,实数a的取值范围是k≥$\frac{5}{2}$或k≤-5.
(3)∵f(x)=-$\frac{1}{2}$x2+x=-$\frac{1}{2}$(x-1)2+$\frac{1}{2}$≤$\frac{1}{2}$.
如果存在满足要求的m,n,则必需3n≤$\frac{1}{2}$,∴n≤$\frac{1}{6}$.
从而m<n≤$\frac{1}{6}$<1,而x≤1,f(x)单调递增,
∴$\left\{\begin{array}{l}{f(m)=-\frac{1}{2}{m}^{2}+m=3m}\\{f(n)=-\frac{1}{2}{n}^{2}+n=3n}\end{array}\right.$,
可解得m=-4,n=0满足要求.
∴存在m=-4,n=0满足要求.
点评 本题考查的知识点是二次函数的性质,其中(1)的关键是由已知条件构造关于a,b的方程组,(2)的关键是转化为函数f(x)在[-2,1]上值域是g(x)在[-2,1]上值域A的子集;(3)的关键是根据函数的值域判断出函数在[m,n]的单调性,进而构造出满足条件的方程.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案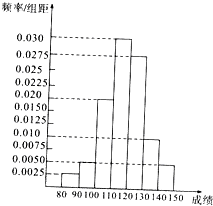 某县有甲乙丙丁四所高中的五千名学生参加了高三的调研测试,为了解数学学科的成绩情况,现从中随机抽取若干名学生在这次测试中的数学成绩作为样本,(其中甲学校抽取了30人),制成如下频率分布表并得到相应的频率分布直方图:
某县有甲乙丙丁四所高中的五千名学生参加了高三的调研测试,为了解数学学科的成绩情况,现从中随机抽取若干名学生在这次测试中的数学成绩作为样本,(其中甲学校抽取了30人),制成如下频率分布表并得到相应的频率分布直方图:| 分组 | 频数 | 频率 |
| [80,90) | 0.025 | |
| [90,100) | 6 | |
| [100,110) | ||
| [110,120) | ||
| [120,130) | ||
| [130,140) | 12 | |
| [140,150) | 0.05 | |
| 合计 |
(2)该次统计中抽取样本的合理方法是什么,甲学校共有多少人参加了调研测试:
(3)从样本在[80,100)的个体中任意抽取2个个体,求至少有一个个体落在[90,100)的概率.
| A. | $({0,\frac{1}{4}}]$ | B. | (0,1) | C. | $[{\frac{1}{4},1})$ | D. | (0,3) |
| 轿车A | 轿车B | 轿车C | |
| 舒适型 | 100 | z | 400 |
| 标准型 | 300 | 450 | 600 |
(1)求z的值;
(2)用分层抽样的方法在B类轿车中抽取一个容量为8的样本,将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率.