题目内容
12. 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=$2\sqrt{2}$.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=$2\sqrt{2}$.(1)求证:BD⊥平面PAC;
(2)求二面角P-CD-B余弦值的大小.
分析 (1)由∠BAD=90°,AD=2,BD=$2\sqrt{2}$.可得AB=2.于是矩形ABCD是正方形,可得BD⊥AC.利用线面垂直的性质可得:PA⊥BD,即可证明:BD⊥平面PAC.
(2)由PA⊥平面ABCD,CD⊥AD,利用三垂线定理可得:CD⊥PD,于是∠PDA是二面角P-CD-B的平面角.利用直角三角形的边角关系即可得出.
解答 (1)证明:∵∠BAD=90°,AD=2,BD=$2\sqrt{2}$.∴$AB=\sqrt{B{D}^{2}-A{D}^{2}}$=2.
∴矩形ABCD是正方形,
∴BD⊥AC.
∵PA⊥平面ABCD,BD?平面ABCD,
∴PA⊥BD,又PA∩AC=A,
∴BD⊥平面PAC.
(2)解:∵PA⊥平面ABCD,CD⊥AD,CD?平面ABCD,
∴CD⊥PD,
∴∠PDA是二面角P-CD-B的平面角.
在Rt△PAD中,tan∠PDA=$\frac{PA}{AD}$=1,
∴∠PDA=45°.
∴二面角P-CD-B的余弦值为$\frac{\sqrt{2}}{2}$.
点评 本题考查了矩形与正方形的性质、线面垂直的性质与判定定理、三垂线定理、二面角、直角三角形的边角关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.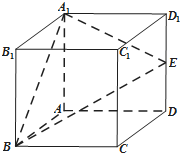 如图,正方体ABCD-A1B1C1D1中,E是棱DD1的中点,F是侧面CDD1C1上的动点,且B1F∥平面A1BE,则B1F与平面CDD1C1所成角的正切值构成的集合是( )
如图,正方体ABCD-A1B1C1D1中,E是棱DD1的中点,F是侧面CDD1C1上的动点,且B1F∥平面A1BE,则B1F与平面CDD1C1所成角的正切值构成的集合是( )
 如图,正方体ABCD-A1B1C1D1中,E是棱DD1的中点,F是侧面CDD1C1上的动点,且B1F∥平面A1BE,则B1F与平面CDD1C1所成角的正切值构成的集合是( )
如图,正方体ABCD-A1B1C1D1中,E是棱DD1的中点,F是侧面CDD1C1上的动点,且B1F∥平面A1BE,则B1F与平面CDD1C1所成角的正切值构成的集合是( )| A. | {2} | B. | {$\frac{{2\sqrt{5}}}{5}$} | C. | [2,2$\sqrt{2}$] | D. | [$\frac{{2\sqrt{5}}}{5}$,2] |
 在如图所示的几何体中,四边形ABCD是正方形,EA⊥底面ABCD,EF∥AD,且AB=6,AE=3$\sqrt{2}$,EF=3.
在如图所示的几何体中,四边形ABCD是正方形,EA⊥底面ABCD,EF∥AD,且AB=6,AE=3$\sqrt{2}$,EF=3.