题目内容
小王有一天收到6位好友分别发来的1,2,2,3,3,4条短信,当天他从这6位好友中任取3位的短信阅读,并且只阅读已选取的好友的全部短信.
(1)求小王当天阅读的短信条数ξ的所有可能取值;
(2)求ξ的数学期望.
(1)求小王当天阅读的短信条数ξ的所有可能取值;
(2)求ξ的数学期望.
(1)设好友A发3条短信,B发2条短信,C发2条短信,D发3条短信,E发3条短信,F发4条短信,
若只阅读好友A、B、C的短信,ξ=5;
若只阅读A、B、D或A、B、E或A、C、D或A、C、E三位好友的短信,ξ=6;
若只阅读A、B、F或A、C、F或B、C、D或B、C、F或A、D、F三位好友的短信,ξ=7;
若只阅读B、C、F或、A、D、F或B、D、E或A、E、F或C、D、E三位好友的短信,ξ=8;
若只阅读B、D、F或C、D、F或B、E、F或C、E、F三位好友的短信,ξ=9;
若只阅读D、E、F三位好友的短信,ξ=10.
故ξ=5,6,7,8,9,10.
(2)由(1)知:
p(ξ=5)=
,p(ξ=6)=
=
,p(ξ=7)=
=
,p(ξ=8)=
=
,p(ξ=9)=
=
,p(ξ=10)=
,
∴ξ的分布列为
∴Eξ=5×
+6×
+7×
+8×
+9×
+10×
=
.
若只阅读好友A、B、C的短信,ξ=5;
若只阅读A、B、D或A、B、E或A、C、D或A、C、E三位好友的短信,ξ=6;
若只阅读A、B、F或A、C、F或B、C、D或B、C、F或A、D、F三位好友的短信,ξ=7;
若只阅读B、C、F或、A、D、F或B、D、E或A、E、F或C、D、E三位好友的短信,ξ=8;
若只阅读B、D、F或C、D、F或B、E、F或C、E、F三位好友的短信,ξ=9;
若只阅读D、E、F三位好友的短信,ξ=10.
故ξ=5,6,7,8,9,10.
(2)由(1)知:
p(ξ=5)=
| 1 |
| 20 |
| 4 |
| 20 |
| 1 |
| 5 |
| 5 |
| 20 |
| 1 |
| 4 |
| 5 |
| 20 |
| 1 |
| 4 |
| 4 |
| 20 |
| 1 |
| 5 |
| 1 |
| 20 |
∴ξ的分布列为
| ξ | 5 | 6 | 7 | 8 | 9 | 10 | ||||||||||||
| P |
|
|
|
|
|
|
| 1 |
| 20 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 20 |
| 15 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

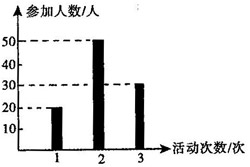
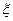 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量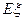 .
.

