题目内容
如图，某小区准备绿化一块直径为AB的半圆形空地，点C在半圆弧上，半圆内△ABC外的地方种草，△ABC的内接正方形PQRS内部为一水池，其余地方种花，若AB=2a，∠CAB=θ，设△ABC的面积为S1，正方形PQRS的边长为x，面积为S2，将比值
称为“规划合理度”．
（1）求证：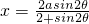
．
（2）当a为定值，θ变化是，求“规划合理度”的最小值及此时角θ的大小．
解：（1）在△ABC中，AB=2a，∠CAB=θ
所以AC=2acosθ，BC=2asinθ
因为正方形PQRS的边长为x
所以AC=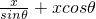
，2acosθ=，
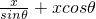∴x=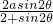
（2）因为△ABC中，AC=2acosθ，BC=2asinθ
所以s1=4a2sinθcosθ=2a2sin2θ
因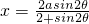
所以s2=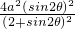
因此“规划合理度”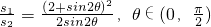
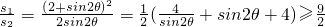
当且仅当sin2θ=1即θ=
时取得最小值
分析：（1）在△ABC中，AB=2a，∠CAB=θ所以AC=2acosθ，BC=2asinθ，再用正方形PQRS的边长为x表示AC=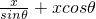，建立2acosθ=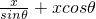求解．
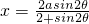（2）由（1）可得s2=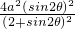建议“规划合理度”模型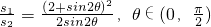，再用基本不等式求解．
点评：本题主要考查平面图形中各边角的量的关系的转化及建立三角模型用基本不等式法或导数求其最值的问题．
所以AC=2acosθ，BC=2asinθ
因为正方形PQRS的边长为x
所以AC=
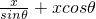，2acosθ=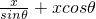，∴x=
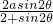
（2）因为△ABC中，AC=2acosθ，BC=2asinθ
所以s1=4a2sinθcosθ=2a2sin2θ
因
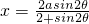
所以s2=
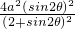
因此“规划合理度”
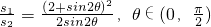
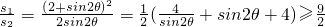
当且仅当sin2θ=1即θ=
时取得最小值分析：（1）在△ABC中，AB=2a，∠CAB=θ所以AC=2acosθ，BC=2asinθ，再用正方形PQRS的边长为x表示AC=
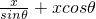，建立2acosθ=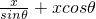求解．（2）由（1）
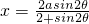可得s2=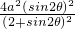建议“规划合理度”模型，再用基本不等式求解．点评：本题主要考查平面图形中各边角的量的关系的转化及建立三角模型用基本不等式法或导数求其最值的问题．
练习册系列答案
相关题目
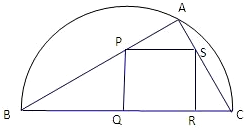如图，某小区准备绿化一块直径为BC的半圆形空地，△ABC外的地方种草，△ABC的内接正方形PQRS为一水池，其余地方种花．若BC=20米，∠ABC=θ，设△ABC的面积为S1，正方形PQRS的面积为S2，将比值
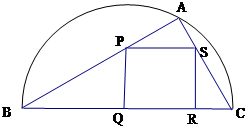如图，某小区准备绿化一块直径为BC的半圆形空地，△ABC的内接正方形PQRS为一水池，△ABC外的地方种草，其余地方种花．若BC=a，∠ABC=θ，设△ABC的面积为S1，正方形PQRS的面积为S2，将比值
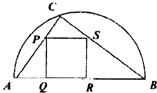如图，某小区准备绿化一块直径为AB的半圆形空地，点C在半圆弧上，半圆内△ABC外的地方种草，△ABC的内接正方形PQRS内部为一水池，其余地方种花，若AB=2a，∠CAB=θ，设△ABC的面积为S1，正方形PQRS的边长为x，面积为S2，将比值
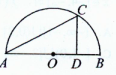如图，某小区准备绿化一块直径为AB的半圆形空地，O为圆心，C为圆周上一点，CD⊥AB于D，△ACD内为一水池，△ACD外栽种花草，若AB=100米，∠CAB=θ，y=AC+CD．
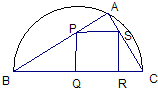（2007•杨浦区二模）如图，某小区准备绿化一块直径为BC的半圆形空地，△ABC外的地方种草，△ABC的内接正方形PQRS为一水池，其余地方种花．若BC=a，∠ABC=θ，设△ABC的面积为S1，正方形PQRS的面积为S2，将比值