题目内容

定义在R上的函数的图象关于点（-
3
4
，0）成中心对称且对任意的实数x都有f（x）=-f（x+
3
2
）且f（-1）=1，f（0）=-2，则f（1）+f（2）+…+f（2010）=（　　）．
A．0B．-2C．-1D．-4
由f（x）=-f（x+
3
2
）得f（x）=f（x+3）即周期为3，
由图象关于点（-
3
4
，0）成中心对称得f（x）+f（-x-
3
2
）=0，
从而-f（x+
3
2
）=-f（-x-
3
2
），所以f（x）=f（-x）．
f（1）=f（4）=…=f（2008）=1，由f（-1）=1，
可得出f（2）=f（5）=…=f（2009）=1，由f（0）=-2，
可得出f（3）=f（6）=…=f（2010）=-2，
故选A
练习册系列答案
相关题目
定义在R上的函数的图象关于点（-
3
4
，0）成中心对称且对任意的实数x都有f（x）=-f（x+
3
2
）且f（-1）=1，f（0）=-2，则f（1）+f（2）+…+f（2010）=（　　）．
A、0B、-2C、-1D、-4
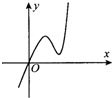精英家教网定义在R上的函数f（x）满足f（4）=1．f′（x）为f（x）的导函数，已知函数y=f′（x）的图象如图所示．若两正数a，b满足f（2a+b）＜1，则
b+2
a+2
的取值范围是（　　）
A、(
1
3
，
1
2
)
B、(-∞，
1
2
)∪(3，+∞)
C、(
1
2
，3)
D、（-∞，-3）
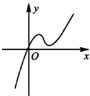定义在R上的函数f（x）满足f（4）=1，f′（x）为f（x）的导函数，已知函数y=f′（x）的图象如图所示．若正数a，b满足f（2a+b）＜1，则
a+2
b+2
的取值范围是（　　）
设定义在R上的函数f(x)=a0x4+a1x3+a2x+a3（a0，a1，a2，a3∈R），当x=-1时，f（x）取极大值
2
3
，且函数y=f（x）的图象关于点（0，0）对称．
（Ⅰ）求f（x）的表达式；
（Ⅱ）试在函数y=f（x）的图象上求两点，使以这两点为切点的切线互相垂直，且切点的横坐标都在[-
2
，
2
]上；
（Ⅲ）设xn∈[
1
2
，1)，ym∈(-
2
，-
2
3
2
]，求证：|f(xn)-f(ym)|＜
4
3
．


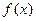对于定义在R上的函数，有下述四个命题，其中正确命题为（  ）
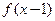①若函数是奇函数，则的图象关于点A（1，0）对称；   
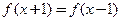②若对x∈R，有，则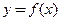的图象关于直线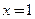对称；      
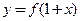③若函数为偶函数，则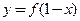的图象关于直线对称；
④函数与函数的图象关于直线对称。
Ａ． ①②④          Ｂ． ①③④           C． ②④         D． ①③   

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网