Question

（13分）

设

   （I）若函数在区间（1，4）内单调递减，求a的取值范围；

   （II）若函数处取得极小值是1，求a的值，并说明在区间（1，4）内函数 的单调性.

 

Answer 1

【答案】

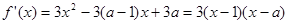                 …………2分

   （1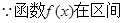）（1，4）内单调递减，

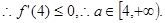                              …………5分

   （2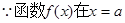）处有极值是1，

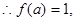
即

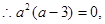所以a=0或3.                           …………8分

当a=0时，f（x）在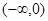上单调递增，

在（0，1）上单调递减，所以f（0）为极大值，

这与函数f（x）在x=a处取得极小值是1矛盾，

所以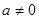                                            …………10分

当a=3时，f（x）在（1，3）上单调递减，在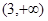上单调递增，

所以f（3）为极小值，

所以a=3时，此时，在区间（1，4）内函数f（x）的单调性是：

f（x）在（1，3）内减，在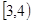内增.                    …………13分

【解析】略