题目内容
已知数列{xn}中,x1=1,xn+1=1+| xn |
| p+xn |
(Ⅰ)当p=2时,用数学归纳法证明xn<
| 2 |
(Ⅱ)是否存在正整数M,使得对于任意正整数n,都有xM≥xn.
分析:(Ⅰ)求出p=2时的表达式,利用数学归纳法的证明步骤,证明不等式,(1)验证n=1不等式成立;(2)假设n=k时成立,证明n=k+1时成立.
(Ⅱ)(1)验证n=1不等式成立;(2)假设n=k时成立,证明n=k+1时成立.
(Ⅱ)(1)验证n=1不等式成立;(2)假设n=k时成立,证明n=k+1时成立.
解答:证明:由x1=1,xn+1=1+
知,xn>0(n∈N*),
(Ⅰ)当p=2时,xn+1=1+
,
(1)当n=1时,x1=1<
,命题成立.
(2)假设当n=k时,xk<
,
则当n=k+1时,xk+1=1+
=2-
<2-
=
,
即n=k+1时,命题成立.
根据(1)(2),xn<
(n∈N*).(4分)
(Ⅱ)用数学归纳法证明,xn+1>xn(n∈N*).
(1)当n=1时,x2=1+
>1=x1,命题成立.
(2)假设当n=k时,xk+1>xk,
∵xk>0,p>0,
∴
<
,
则当n=k+1时,xk+1=1+
=2-
<2-
=xk+2,
即n=k+1时,命题成立.
根据(1)(2),xn+1>xn(n∈N*).(8分)
故不存在正整数M,使得对于任意正整数n,都有xM≥xn.(10分)
| xn |
| p+xn |
(Ⅰ)当p=2时,xn+1=1+
| xn |
| 2+xn |
(1)当n=1时,x1=1<
| 2 |
(2)假设当n=k时,xk<
| 2 |
则当n=k+1时,xk+1=1+
| xk |
| 2+xk |
| 2 |
| 2+xk |
| 2 | ||
2+
|
| 2 |
即n=k+1时,命题成立.
根据(1)(2),xn<
| 2 |
(Ⅱ)用数学归纳法证明,xn+1>xn(n∈N*).
(1)当n=1时,x2=1+
| x1 |
| p+x1 |
(2)假设当n=k时,xk+1>xk,
∵xk>0,p>0,
∴
| p |
| p+xk+1 |
| p |
| p+xk |
则当n=k+1时,xk+1=1+
| xk |
| p+xk |
| p |
| p+xk |
| p |
| p+xk+1 |
即n=k+1时,命题成立.
根据(1)(2),xn+1>xn(n∈N*).(8分)
故不存在正整数M,使得对于任意正整数n,都有xM≥xn.(10分)
点评:本题是中档题,考查数学归纳法的证明步骤,注意证明的过程两步骤缺一不可,注意形式的一致性,考查计算能力.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
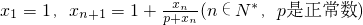 .
.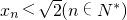
 .
.