题目内容
已知数列{xn}中,x1,x5是方程log22x-8log2x+12=0的两根,等差数列{yn}满足yn=log2xn,且其公差为负数,
(1)求数列{yn}的通项公式;
(2)证明:数列{xn}为等比数列;
(3)设数列{xn}的前n项和为Sn,若对一切正整数n,Sn<a恒成立,求实数a的取值范围.
(1)求数列{yn}的通项公式;
(2)证明:数列{xn}为等比数列;
(3)设数列{xn}的前n项和为Sn,若对一切正整数n,Sn<a恒成立,求实数a的取值范围.
分析:(1)由x1,x5是方程log22x-8log2x+12=0的两根,等差数列{yn}满足yn=log2xn,且其公差为负数,能够推导出y1=log2x1=6,y5=log2x5=2,yn=7-n.
(2)由yn=log2xn=7-n,yn+1=log2xn+1=6-n,知
=
=
,由此能够证明数列{xn}为等比数列.
(3)Sn=
=128(1-
)<128
Sn=128,由此能求出a的取值范围.
(2)由yn=log2xn=7-n,yn+1=log2xn+1=6-n,知
| xn+1 |
| xn |
| 26-n |
| 27-n |
| 1 |
| 2 |
(3)Sn=
26(1-
| ||
1-
|
| 1 |
| 2n |
| lim |
| n→∞ |
解答:解:(1)∵x1,x5是方程log22x-8log2x+12=0的两根,
∴log2x1+log2x5=8,log2x1•log2x5=12,
∵等差数列{yn}满足yn=log2xn,且其公差为负数,
∴log2x1=6,log2x5=2.
y1=log2x1=6,y5=log2x5=2,yn=7-n.
(2)∵yn=log2xn=7-n,yn+1=log2xn+1=6-n
∴
=
=
,
∴数列{xn}为等比数列.
(3)Sn=
=128(1-
)<128
Sn=128,
故所求a的取值范围为a≥128.
∴log2x1+log2x5=8,log2x1•log2x5=12,
∵等差数列{yn}满足yn=log2xn,且其公差为负数,
∴log2x1=6,log2x5=2.
y1=log2x1=6,y5=log2x5=2,yn=7-n.
(2)∵yn=log2xn=7-n,yn+1=log2xn+1=6-n
∴
| xn+1 |
| xn |
| 26-n |
| 27-n |
| 1 |
| 2 |
∴数列{xn}为等比数列.
(3)Sn=
26(1-
| ||
1-
|
| 1 |
| 2n |
| lim |
| n→∞ |
故所求a的取值范围为a≥128.
点评:本题考查通项公式的求法、等比数列的证明和实数a的取值的求法,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
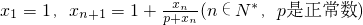 .
.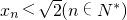
 .
.