题目内容
下列函数 中,满足“对任意的
中,满足“对任意的 时,都有
时,都有 ”的是( )
”的是( )
A. | B. |
C. | D. |
C
解析试题分析:对任意 ,都有f(x1)<f(x2),即说明f(x)在
,都有f(x1)<f(x2),即说明f(x)在 上单调递增,而
上单调递增,而 ,
, 在区间
在区间 上均单调递减,
上均单调递减,
在 (-∞,2)是减函数,在(2,+∞)是增函数,只有函数 是单调递增函数,
是单调递增函数,
故选C。
考点:常见函数的单调性
点评:简单题,熟练掌握常见函数的单调性,是解题的关键。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若定义在R上的偶函数 满足
满足 且
且 时,
时, 则方程
则方程 的零点个数是( )
的零点个数是( )
| A.2个 | B.3个 | C.4个 | D.多于4个 |
偶函数 则关于
则关于 的方程
的方程 上解的个数是( )
上解的个数是( )
| A.l | B.2 | C.3 | D.4 |
函数 .满足
.满足 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
下列各组函数是同一函数的是( )
A. 与 与 | B. 与 与 |
C.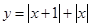 与 与 | D. 与 与 |
(5分)设函数 (a∈R,e为自然对数的底数).若存在b∈[0,1]使f(f(b))=b成立,则a的取值范围是( )
(a∈R,e为自然对数的底数).若存在b∈[0,1]使f(f(b))=b成立,则a的取值范围是( )
| A.[1,e] | B.[1,1+e] | C.[e,1+e] | D.[0,1] |
 在区间
在区间 上的简图是( )
上的简图是( )
 上为增函数,且
上为增函数,且 ,则不等式
,则不等式 的解集为( ).
的解集为( ). 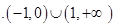



 中,
中, ,且
,且 ,设
,设 =
= ,
, ),以
),以 为焦点且过点
为焦点且过点 的双曲线的离心率为
的双曲线的离心率为 ,以
,以 为焦点且过点
为焦点且过点 的椭圆的离心率为
的椭圆的离心率为 ,设
,设 的大致图像是( )
的大致图像是( ) 
