题目内容
已知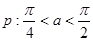 ,
,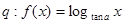 在
在 内是增函数,则p是q的( )
内是增函数,则p是q的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
解析试题分析:因为由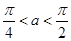 可得
可得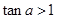 .所以函数
.所以函数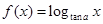 在
在 内是增函数.所以p是q的充分条件.又因为若函数
内是增函数.所以p是q的充分条件.又因为若函数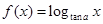 在
在 内是增函数,则
内是增函数,则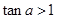 .
. .所以q不是p的充分条件.由此可得.p是q的充分不必要条件.故选A.
.所以q不是p的充分条件.由此可得.p是q的充分不必要条件.故选A.
考点:1.三角形函数的知识.2.对数函数的单调性.3.复合函数的单调性.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
下列命题为真命题的是( )
A.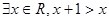 | B.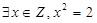 |
C.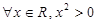 | D.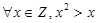 |
己知实数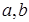 满足
满足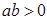 ,则“
,则“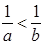 成立”是“
成立”是“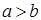 成立”的( ).
成立”的( ).
| A.充分非必要条件. | B.必要非充分条件. |
| C.充要条件. | D.既非充分又非必要条件. |
“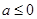 ”是“函数
”是“函数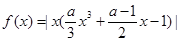 在区间
在区间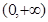 上单调递增”的( )
上单调递增”的( )
| A.充分必要条件 | B.必要不充分条件 |
| C.充分不必要条件 | D.既不充分也不必要条件 |
设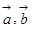 为向量。则
为向量。则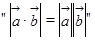 是
是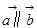 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也必要条件 |
设向量 ,
,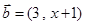 ,则“
,则“ ∥
∥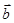 ”是“
”是“ ”的( )
”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充分必要条件 | D.既非充分又非必要条件 |
“|x-1|<2成立”是“x(x-3)<0成立”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
设 ,则“
,则“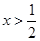 ”是“
”是“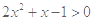 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知命题 ,则( )
,则( )
A. | B. |
C. | D. |