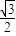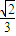题目内容
已知椭圆方程为C:
+y2=1,它的左、右焦点分别为F1、F2.点P(x0,y0)为第一象限内的点.直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点.
(1)求椭圆上的点与两焦点连线的最大夹角;
(2)设直线PF1、PF2的斜率分别为k1、k2.试找出使得直线OA、OB、OC、OD的斜率kOA、kOB、kOC、kOD满足kOA+kOB+kOC+kOD=0成立的条件(用k1、k2表示).
(3)又已知点E为抛物线y2=2px(p>0)上一点,直线F2E与椭圆C的交点G在y轴的左侧,且满足
=2
,求p的最大值.
| x2 |
| 2 |
(1)求椭圆上的点与两焦点连线的最大夹角;
(2)设直线PF1、PF2的斜率分别为k1、k2.试找出使得直线OA、OB、OC、OD的斜率kOA、kOB、kOC、kOD满足kOA+kOB+kOC+kOD=0成立的条件(用k1、k2表示).
(3)又已知点E为抛物线y2=2px(p>0)上一点,直线F2E与椭圆C的交点G在y轴的左侧,且满足
| EG |
| F2E |
分析:(1)利用椭圆的定义,结合余弦定理、基本不等式,即可求得椭圆上的点与两焦点连线的最大夹角;
(2)设出A,B,C,D的坐标,联立直线PF1和椭圆的方程根据韦达定理表示出xA+xB和xAxB,进而可求得直线OA,OB斜率的和与CO,OD斜率的和,由kOA+k)B+kOC+kOD=0推断出k1+k2=0或k1k2=1;
(3)设出G的坐标,可得E的坐标,利用E在抛物线上,可得p的函数,换元,利用基本不等,即可得到结论.
(2)设出A,B,C,D的坐标,联立直线PF1和椭圆的方程根据韦达定理表示出xA+xB和xAxB,进而可求得直线OA,OB斜率的和与CO,OD斜率的和,由kOA+k)B+kOC+kOD=0推断出k1+k2=0或k1k2=1;
(3)设出G的坐标,可得E的坐标,利用E在抛物线上,可得p的函数,换元,利用基本不等,即可得到结论.
解答:解:(1)由题意,设椭圆上的点与两焦点连线的距离为m,n,夹角为α,则m+n=2
∴cosα=
=
-1
∵m+n=2
≥2
∴0<mn≤2
∴
-1≥0
∴cosα≥0
∴当m=n时,椭圆上的点与两焦点连线的最大夹角为90°;
(2)设直线PF1、PF2的方程分别为y=k1(x+1),y=k2(x-1),A(xA,yA),B(xB,yB),C(xC,yC),D(xD,yD),
联立直线PF1和椭圆的方程化简得(2k12+1)x2+4k12x+2k12-2=0,
因此xA+xB=-
,xAxB=
,所以kOA+kOB=
+
=-
同理可得:kOC+kOD=-
,
故由kOA+kOB+kOC+kOD=0得k1+k2=0或k1k2=1;
(3)F2(1,0),设G(x0,y0),(-
≤x0≤0),则
∵
=2
,∴xE=
,yE=
,
∵E为抛物线y2=2px(p>0)上一点,
∴(
)2=2p•
∵
+y02=1
∴12p=
令t=x0+2,则2-
≤t<2
∴12p=-(t+
-4)≤-(2
-4),∴p≤
-
,当且仅当t=
时,取等号
∴x0=
-2时,p的最大值为
-
.
| 2 |
∴cosα=
| m2+n2-4 |
| 2mn |
| 2 |
| mn |
∵m+n=2
| 2 |
| mn |
∴0<mn≤2
∴
| 2 |
| mn |
∴cosα≥0
∴当m=n时,椭圆上的点与两焦点连线的最大夹角为90°;
(2)设直线PF1、PF2的方程分别为y=k1(x+1),y=k2(x-1),A(xA,yA),B(xB,yB),C(xC,yC),D(xD,yD),
联立直线PF1和椭圆的方程化简得(2k12+1)x2+4k12x+2k12-2=0,
因此xA+xB=-
| 4k12 |
| 2k12+1 |
| 2k12-2 |
| 2k12+1 |
| yA |
| xA |
| yB |
| xB |
| 2k1 |
| k12-1 |
同理可得:kOC+kOD=-
| 2k2 |
| k22-1 |
故由kOA+kOB+kOC+kOD=0得k1+k2=0或k1k2=1;
(3)F2(1,0),设G(x0,y0),(-
| 2 |
∵
| EG |
| F2E |
| x0+2 |
| 3 |
| y0 |
| 3 |
∵E为抛物线y2=2px(p>0)上一点,
∴(
| y0 |
| 3 |
| x0+2 |
| 3 |
∵
| x02 |
| 2 |
∴12p=
| 2-x02 |
| x0+2 |
令t=x0+2,则2-
| 2 |
∴12p=-(t+
| 2 |
| t |
| 2 |
| 1 |
| 3 |
| ||
| 6 |
| 2 |
∴x0=
| 2 |
| 1 |
| 3 |
| ||
| 6 |
点评:本题考查椭圆的定义,考查余弦定理、考查基本不等式的运用,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,属于难题.

练习册系列答案
相关题目
 ,A、B分别是椭圆长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,若
,A、B分别是椭圆长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,若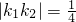 ,则椭圆的离心率为
,则椭圆的离心率为



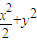 =1,它的左、右焦点分别为F1、F2.点P(x,y)为第一象限内的点.直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点.
=1,它的左、右焦点分别为F1、F2.点P(x,y)为第一象限内的点.直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点.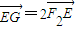 ,求p的最大值.
,求p的最大值.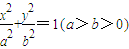 ,A、B分别是椭圆长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,若
,A、B分别是椭圆长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,若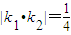 ,则椭圆的离心率为( )
,则椭圆的离心率为( )