题目内容
设F为椭圆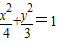 的右焦点,则该椭圆上与点F的距离最远的点到椭圆右准线的距离为( )
的右焦点,则该椭圆上与点F的距离最远的点到椭圆右准线的距离为( )A.2
B.5
C.6
D.20
【答案】分析:由于该椭圆上与点F的距离最远的点为左顶点,所以椭圆上与点F的距离最远的点到椭圆右准线的距离,即为椭圆的左顶点到椭圆右准线的距离,根据抛物线的标准方程易求.
解答:解:由题意,根据椭圆的标准方程可知,左顶点坐标为(-2,0),右准线方程为
∵该椭圆上与点F的距离最远的点为左顶点
∴该椭圆上与点F的距离最远的点到椭圆右准线的距离为4+2=6
故选C.
点评:本题以椭圆为载体,主要考查椭圆的几何性质,关键是注意该椭圆上与点F的距离最远的点为左顶点.
解答:解:由题意,根据椭圆的标准方程可知,左顶点坐标为(-2,0),右准线方程为

∵该椭圆上与点F的距离最远的点为左顶点
∴该椭圆上与点F的距离最远的点到椭圆右准线的距离为4+2=6
故选C.
点评:本题以椭圆为载体,主要考查椭圆的几何性质,关键是注意该椭圆上与点F的距离最远的点为左顶点.

练习册系列答案
相关题目
 的右焦点,则该椭圆上与点F的距离最远的点到椭圆右准线的距离为
的右焦点,则该椭圆上与点F的距离最远的点到椭圆右准线的距离为 的右焦点,过椭圆中心作一直线与椭圆交于P,Q两点,当三角形PFQ的面积最大时,
的右焦点,过椭圆中心作一直线与椭圆交于P,Q两点,当三角形PFQ的面积最大时,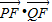 的值为 .
的值为 .