题目内容
1.在满足极坐标和直角坐标互化条件下,极坐标方程ρ2=$\frac{12}{3co{s}^{2}θ+4si{n}^{2}θ}$经过直角坐标系下的伸缩变换$\left\{\begin{array}{l}{x′=\frac{1}{2}x}\\{y′=\frac{\sqrt{3}}{3}y}\end{array}\right.$后,得到的曲线是( )| A. | 直线 | B. | 椭圆 | C. | 双曲线 | D. | 圆 |
分析 先把极坐标方程化为直角坐标方程,再经过直角坐标系下的伸缩变换,把直角坐标方程中的x,y分别换成得$2{x}^{'},\sqrt{3}{y}^{'}$,由此能求出结果.
解答 解:∵极坐标方程ρ2=$\frac{12}{3co{s}^{2}θ+4si{n}^{2}θ}$,
∴3ρ2cos2θ+4ρ2sin2θ=12,
∴直角坐标方程为:3x2+4y2=12,
即$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,
∴经过直角坐标系下的伸缩变换$\left\{\begin{array}{l}{x′=\frac{1}{2}x}\\{y′=\frac{\sqrt{3}}{3}y}\end{array}\right.$后,
得到的曲线方程为$\frac{(2{x}^{'})^{2}}{4}+\frac{(\sqrt{3}{y}^{'})^{2}}{3}$=12,即x'2+y'2=12,
∴得到的曲线是圆.
故选:D.
点评 本题考查曲线形状的判断,是基础题,解题时要认真审题,注意极坐标方程、直角坐标方程和直角坐标系下的伸缩变换公式的合理运用.

练习册系列答案
相关题目
10.在空间直角坐标系中,点P(3,1,5)关于yOz平面对称的点的坐标为( )
| A. | (-3,1,5) | B. | (-3,-1,5) | C. | (3,-1,-5) | D. | (-3,1,-5) |
11.(1+tan12°)(1-tan147°)=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
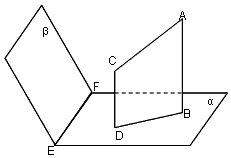 假设平面α∩平面β=EF,AB⊥α,CD⊥β,垂足分别为B,D,若增加一个条件,就能推出BD⊥EF.现有下面四个条件:
假设平面α∩平面β=EF,AB⊥α,CD⊥β,垂足分别为B,D,若增加一个条件,就能推出BD⊥EF.现有下面四个条件: