题目内容
若M={x|x=in,n∈Z},N={x|
>-1}(其中i为虚数单位),则M∩(CRN)=( )
| 1 |
| x |
| A、{-1,1} | B、{-1} |
| C、{-1,0} | D、{1} |
分析:先用列举法写出集合M={1,-1,i,-i},化简集合N,求出集合N的补集,再求与集合M的交集.
解答:解:依题意M={1,-1,i,-i},
N={x|x>0或x<-1},
所以CRN={x|-1≤x≤0},故M∩(CRN)={-1}.故选B
N={x|x>0或x<-1},
所以CRN={x|-1≤x≤0},故M∩(CRN)={-1}.故选B
点评:本题属于以复数与不等式为依托,求集合的交集的基础题,也是高考常会考的题型.

练习册系列答案
相关题目
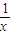 >-1}(其中i为虚数单位),则M∩(CRN)=( )
>-1}(其中i为虚数单位),则M∩(CRN)=( )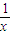 >-1}(其中i为虚数单位),则M∩(CRN)=( )
>-1}(其中i为虚数单位),则M∩(CRN)=( ) >-1}(其中i为虚数单位),则M∩(CRN)=
>-1}(其中i为虚数单位),则M∩(CRN)=