题目内容
已知平面上两个定点 、
、 ,P为一个动点,且满足
,P为一个动点,且满足
 .
.(1)求动点P的轨迹C的方程;
(2)若A、B是轨迹C上的两个不同动点
 .分别以A、B为切点作轨迹C的切线,设其交点为Q,证明
.分别以A、B为切点作轨迹C的切线,设其交点为Q,证明 为定值.
为定值.
【答案】分析:(1)先设P(x,y),欲动点P的轨迹C的方程,即寻找x,y之间的关系,结合向量的坐标运算即可得到.
(2)先设出A,B两点的坐标,利用向量关系及向量运算法则,用A,B的坐标表示出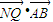 ,最后看其是不是定值即可.
,最后看其是不是定值即可.
解答:解:(I)设P(x,y).
由已知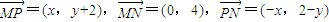 ,
,
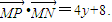
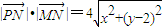 (3分)
(3分)
∵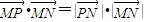
∴4y+8=4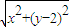 整理,得x2=8y
整理,得x2=8y
即动点P的轨迹C为抛物线,其方程为x2=8y.(6分)
(II)由已知N(0,2).
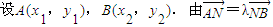
即得(-x1,2-y1)=λ(x2,y2-2)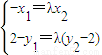
将(1)式两边平方并把x12=8y1,x22=8y2代入得y1=λ2y2(3分)
解(2)、(3)式得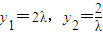 ,
,
且有x1x2=-λx22=-8λy2=-16.(8分)
抛物线方程为 .
.
所以过抛物线上A、B两点的切线方程分别是
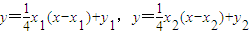 ,
,
即y=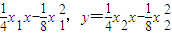
解出两条切线的交点Q的坐标为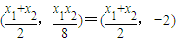 (11分)
(11分)
所以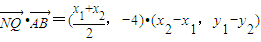
=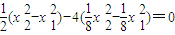
所以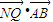 为定值,其值为0.(13分)
为定值,其值为0.(13分)
点评:求曲线的轨迹方程是解析几何的基本问题 求符合某种条件的动点的轨迹方程,其实质就是利用题设中的几何条件,用“坐标化”将其转化为寻求变量间的关系.
(2)先设出A,B两点的坐标,利用向量关系及向量运算法则,用A,B的坐标表示出
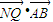 ,最后看其是不是定值即可.
,最后看其是不是定值即可.解答:解:(I)设P(x,y).
由已知
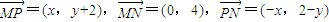 ,
,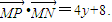
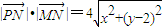 (3分)
(3分)∵
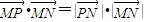
∴4y+8=4
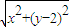 整理,得x2=8y
整理,得x2=8y即动点P的轨迹C为抛物线,其方程为x2=8y.(6分)
(II)由已知N(0,2).
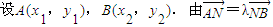
即得(-x1,2-y1)=λ(x2,y2-2)
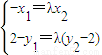
将(1)式两边平方并把x12=8y1,x22=8y2代入得y1=λ2y2(3分)
解(2)、(3)式得
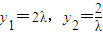 ,
,且有x1x2=-λx22=-8λy2=-16.(8分)
抛物线方程为
 .
.所以过抛物线上A、B两点的切线方程分别是
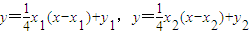 ,
,即y=
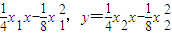
解出两条切线的交点Q的坐标为
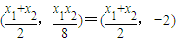 (11分)
(11分)所以
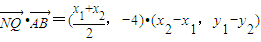
=
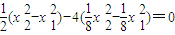
所以
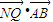 为定值,其值为0.(13分)
为定值,其值为0.(13分)点评:求曲线的轨迹方程是解析几何的基本问题 求符合某种条件的动点的轨迹方程,其实质就是利用题设中的几何条件,用“坐标化”将其转化为寻求变量间的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目